
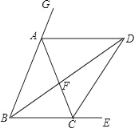
【题目】如图,已知在△ABC中,AD、BD分别平分∠CAG、∠EBA,AD∥BC,BD交AC于F,连接CD,
(1)求证:AB=AC.
(2)当∠EBA的大小满足什么条件时,以A,B,F为顶点三角形为等腰三角形?
(3)猜想∠BDC与∠DAC之间的数量关系式,并说明理由.
【答案】(1)详见解析;(2)∠EBA=72°或![]() 时,△ABF为等腰三角形;(3)∠BDC+∠DAC=90°.
时,△ABF为等腰三角形;(3)∠BDC+∠DAC=90°.
【解析】
(1)根据平行线的性质可得∠GAD=∠ABC,∠ACB=∠CAD,即∠ABC=∠ACB,则AB=AC;
(2)分①AB与AF不可能相等;②当AF=BF时,③AB=BF时,三种情况讨论,根据三角形的内角和定理进行求解即可;
(3)作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H,根据三角形的外角等于其不相邻的两个内角和,可得∠BDC=∠DCH﹣∠DBH=![]() ∠ACH﹣
∠ACH﹣![]() ∠ABH=
∠ABH=![]() (∠ACH﹣∠ABH)=
(∠ACH﹣∠ABH)=![]() ∠BAC,因为∠DAC=
∠BAC,因为∠DAC=![]() ×(180°﹣∠A)=90°﹣
×(180°﹣∠A)=90°﹣![]() ∠BAC,所以∠BDC+∠DAC=90°.
∠BAC,所以∠BDC+∠DAC=90°.
(1)证明:∵AD平分∠CAG,
∴∠GAD=∠CAD,
∵AD∥BC,
∴∠GAD=∠ABC,∠ACB=∠CAD,
∴∠ABC=∠ACB,
∴AB=AC;
(2))①AB与AF不可能相等;
②当AF=BF时,∠BAF=∠ABF=![]() ∠ABC,
∠ABC,
∵∠BAC+∠ABC+∠ACB=180°,∠ABC=∠ACB,
∴![]() ∠ABC=180°,
∠ABC=180°,
∴∠ABC=72°;
③AB=BF时,设∠ABF=∠FBC=x,
则∠ABC=∠ACB=2x,
∴∠BAF=∠BFA=3x,
∴2x+2x+3x=180°,
∴x=![]() ,
,
∴∠EBA=2x=![]() ,
,
综上所述,当∠EBA=72°或![]() 时,△ABF为等腰三角形;
时,△ABF为等腰三角形;
(3)∠BDC+∠DAC=90°,
理由如下:作DM⊥BG于M,DN⊥AC于N,DH⊥BE于H,
∵AD、BD分别平分∠GAC、∠EBA,DM⊥BG,DN⊥AC,DH⊥BE,
∴DM=DN,DM=DH,
∴DH=DN,
又∵DN⊥AC,DH⊥BE,
∴CD平分∠ADH,即∠DCH=![]() ∠ACH,
∠ACH,
∴∠BDC=∠DCH﹣∠DBH=![]() ∠ACH﹣
∠ACH﹣![]() ∠ABH=
∠ABH=![]() (∠ACH﹣∠ABH)=
(∠ACH﹣∠ABH)=![]() ∠BAC,
∠BAC,
∵∠DAC=![]() ×(180°﹣∠A)=90°﹣
×(180°﹣∠A)=90°﹣![]() ∠BAC,
∠BAC,
∴∠BDC+∠DAC=90°.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,某地在山区修建高速公路时需挖通一条隧道,为估计这条隧道的长度需测出这座山A、B间的距离,结合所学知识或方法,设计测量方案你能给出什么好的方法吗?

查看答案和解析>>
科目:初中数学 来源: 题型:
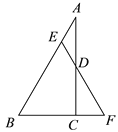
【题目】如图,在 Rt△ABC 中,∠A=30°,∠ACB=90°,点 D 为 AC 中点, 点 E 为 AB 边上一动点,AE=DE,延长 ED 交 BC 的延长线于点 F.
(1)求证:△BEF 是等边三角形;
(2)若 AB=12,求 DE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,请仔细观察并找出规律,解答下列问题:

(1)按照此规律,摆第n个图时,需用火柴棒的根数是多少?
(2)求摆第50个图时所需用的火柴棒的根数;
(3)按此规律用1202根火柴棒摆出第n个图形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l与⊙O相离,OA⊥l于点A,交⊙O于点P,点B是⊙O上一点,连接BP并延长,交直线l于点C,使得AB=AC. 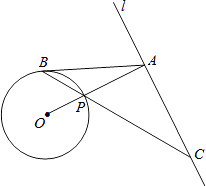
(1)求证:AB是⊙O的切线;
(2)PC=2 ![]() ,OA=4. ①求⊙O的半径;
,OA=4. ①求⊙O的半径;
②求线段PB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①BE= ![]() AC;②∠A=∠EBA;③EB平分∠AED;④ED=
AC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 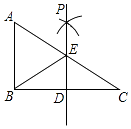
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AD平分∠BAC,DE⊥AB,DF⊥AC,E、F分别为垂足,则下列四个结论:①∠DEF=∠DFE; ②AE=AF; ③AD平分∠EDF; ④AD垂直平分EF.其中正确结论有()
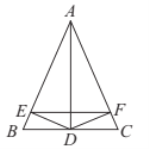
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雷达二维平面定位的主要原理是:测量目标的两个信息―距离和角度,目标的表示方法为![]() ,其中,m表示目标与探测器的距离;
,其中,m表示目标与探测器的距离;![]() 表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为
表示以正东为始边,逆时针旋转后的角度.如图,雷达探测器显示在点A,B,C处有目标出现,其中,目标A的位置表示为![]() ,目标C的位置表示为
,目标C的位置表示为![]() .用这种方法表示目标B的位置,正确的是( )
.用这种方法表示目标B的位置,正确的是( )

A. (-4, 150°) B. (4, 150°) C. (-2, 150°) D. (2, 150°)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com