
【题目】如图,在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①BE= ![]() AC;②∠A=∠EBA;③EB平分∠AED;④ED=
AC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 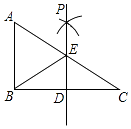
A.①②③
B.①②④
C.①③④
D.②③④
【答案】B
【解析】解:∵由作图可得P到B、C两点距离相等, 又∵点D是BC边的中点,
∴PD是BC的垂直平分线,
∴DE是△ABC的中位线,
∴E是AC的中点,
∴BE= ![]() AC,故①正确;
AC,故①正确;
∵PD是BC的垂直平分线,
∴EB=EC,
∴∠C=∠EBC,
∵∠ABC=90°,
∴∠A+∠C=90°,∠ABE+∠EBC=90°,
∴∠A=∠EBA,故②正确;
根据所给条件无法证明EB平分∠AED,故③错误;
∵∠A=∠EBA,
∴AE=BE,
∵BE=EC,
∴EA=EC,
∵D为BC中点,
∴DE是△ABC的中位线,
∴ED= ![]() AB,故④正确.
AB,故④正确.
故选B.
根据作图可得P到B、C两点距离相等,再由D是BC边的中点可得PD是BC的垂直平分线,由三角形中位线定理及直角三角形的性质可得①正确;再根据角的互余关系可证明∠A=∠EBA,故②正确;结论③不能证明,根据三角形中位线定理可得④正确.


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC、△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C、D、E三点在同一直线上,连接BD.
(1)求证:△BAD≌△CAE;
(2)试猜想BD、CE有何特殊位置关系,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,平移三角形ABD,使点D沿BD的延长线平移至点C,得到三角形![]() ,
,![]() 交AC于点E,AD平分∠BAC.
交AC于点E,AD平分∠BAC.
(1)猜想![]() 与
与![]() 之间的关系,并写出理由;
之间的关系,并写出理由;
(2)如果将三角形ABD平移至如图2所示位置,得到三角形![]() ,请问
,请问![]() 平分
平分![]() 吗?为什么?
吗?为什么?
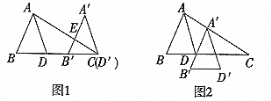
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AC的垂直平分线上.
(1)若AB=AD,∠BAD=26°,求∠B和∠C的度数;
(2)若AB=AD=DC,AC=BC,求∠C的度数;
(3)若AC=6,△ABD的周长为13cm,求△ABC的周长.
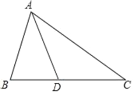
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,AD、BD分别平分∠CAG、∠EBA,AD∥BC,BD交AC于F,连接CD,
(1)求证:AB=AC.
(2)当∠EBA的大小满足什么条件时,以A,B,F为顶点三角形为等腰三角形?
(3)猜想∠BDC与∠DAC之间的数量关系式,并说明理由.
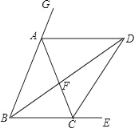
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正整数按如图所示的规律在平面直角坐标系中进行排列,每个正整数对应一个整点坐标(x,y),且x,y均为整数,如数5对应的坐标为(-1,1),试探求2015对应的坐标.
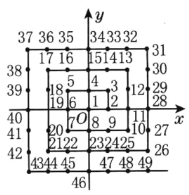
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一块广告牌AB顶端固定在一堵墙AD的A点处,与地面夹角∠ABD=45°,由于施工底部断裂掉一段以后,底部落在距离B点8米处的C点,此时与地面夹角∠ACD=75°.求断裂前、后的广告牌AB、AC的长度. 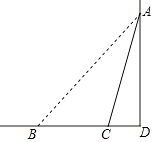
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强是校学生会体育部部长,他想了解现在同学们更喜欢什么球类运动,以便学生会组织受欢迎的比赛.于是他设计了调查问卷,在全校每个班都随机选取了一定数量的学生进行调查,调查问卷如下:
调查问卷
你最喜欢的球类运动是( )(单选)
A、篮球B、足球C、排球D、乒乓球E、羽毛球F、其他
调查问卷
你最喜欢的球类运动是( )(单选)
A、篮球B、足球C、排球D、乒乓球E、羽毛球F、其他
小强根据统计数据制作的各活动小组人数分布情况的统计表和扇形统计图如下
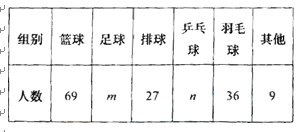

(1)请你写出统计表中空缺部分的人数m= , n= .
(2)在扇形统计图中,羽毛球所对应的扇形圆心角等于 .
(3)请你根据调查结果,给小强部长简要提出两条合理化的建议.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com