
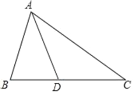
【题目】如图,在△ABC中,点D在AC的垂直平分线上.
(1)若AB=AD,∠BAD=26°,求∠B和∠C的度数;
(2)若AB=AD=DC,AC=BC,求∠C的度数;
(3)若AC=6,△ABD的周长为13cm,求△ABC的周长.
【答案】(1)∠B=77°,∠C=38.5°;(2)36°;(3)19cm.
【解析】
(1)根据题意在等腰三角形BAD中求得∠ADB的度数,根据垂直平分线的性质得到AD=CD,即∠DAC=∠C,再根据三角形的外角等于不相邻的两个内角和即可得解;
(2)设∠B=x°,根据等腰三角形的性质得到关于x的方程,x+x+![]() x=180,然后求解方程,最后求得∠C的度数即可;
x=180,然后求解方程,最后求得∠C的度数即可;
(3)根据垂直平分线的性质得到AD=CD,然后将相关线段相加即可得解.
解:(1)在△ABD中,
∵AB=AD,∠BAD=26°,
∴∠B=∠ADB=(180°﹣26°)×![]() =77°,
=77°,
又∵点D在AC的垂直平分线上,
∴AD=DC,
∴∠C=![]() 77°=38.5°;
77°=38.5°;
(2)设∠B=x°,
∵CA=CB,
∴∠A=∠CAB=x°,
∵AB=AD=DC,
∴∠B=∠ABD=x°,∠C=![]() x°,
x°,
在△ABC中,x+x+![]() x=180,
x=180,
解得:x=72,
∴∠C=![]() ×72°=36°.
×72°=36°.
故∠C的度数是36°;
(3)∵点D在AC的垂直平分线上,
∴DA=DC,
∵△ABD的周长为13cm
∴AB+BD+AD=13cm,
即AB+BD+DC=13cm,
∴AB+BC+AC=13+6=19cm,
∴△ABC的周长为19cm.


科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题,
例题:若m2+2mn+2n2﹣6n+9=0,求m和n的值.
解:∵m2+2mn+2n2﹣6n+9=0
∴m2+2mn+n2+n2﹣6n+9=0
∴(m+n)2+(n﹣3)2=0
∴m+n=0,n﹣3=0
∴m=﹣3,n=3
问题(1)若x2+2y2﹣2xy+4y+4=0,求xy的值.
(2)已知a,b,c是△ABC的三边长,满足a2+b2=10a+8b﹣41,且c是△ABC中最长的边,求c的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=mx2+(m2﹣m)x﹣2m+1的图象与x轴交于点A、B,与y轴交于点C,顶点D的横坐标为1.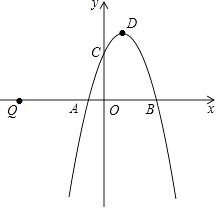
(1)求二次函数的表达式及A、B的坐标;
(2)若P(0,t)(t<﹣1)是y轴上一点,Q(﹣5,0),将点Q绕着点P顺时针方向旋转90°得到点E.当点E恰好在该二次函数的图象上时,求t的值;
(3)在(2)的条件下,连接AD、AE.若M是该二次函数图象上一点,且∠DAE=∠MCB,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程(n-2)x2m+3+3y5|n|-9=4.
(1)若方程是二元一次方程,求m2+n2的值;
(2)若方程是一元一次方程,求m,n的值或取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某幼儿园举行用火柴棒摆“金鱼”比赛,如图所示,请仔细观察并找出规律,解答下列问题:

(1)按照此规律,摆第n个图时,需用火柴棒的根数是多少?
(2)求摆第50个图时所需用的火柴棒的根数;
(3)按此规律用1202根火柴棒摆出第n个图形,求n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
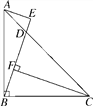
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,D是AC上一点,AE⊥BD,交BD的延长线于E,CF⊥BD于F.
(1)求证:CF=BE;
(2)若BD=2AE,求证:∠EAD=∠ABE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,点D是BC边的中点,分别以B、C为圆心,大于线段BC长度一半的长为半径画弧,两弧在直线BC上方的交点为P,直线PD交AC于点E,连接BE,则下列结论:①BE= ![]() AC;②∠A=∠EBA;③EB平分∠AED;④ED=
AC;②∠A=∠EBA;③EB平分∠AED;④ED= ![]() AB中,一定正确的是( )
AB中,一定正确的是( ) 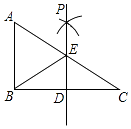
A.①②③
B.①②④
C.①③④
D.②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系中,抛物线y=ax2+bx+2过点A(﹣3,0)、B (1,0),与y轴交于点C,抛物线的顶点为D,点G在抛物线上且其纵坐标为2.
(1)a= , b= , D( , ).
(2)P是线段AB上一动点(点P不与A、B重合),点P作x轴的垂线交抛物线于点E.
①若PE=PB,试求E点坐标;
②在①的条件下,PE、DG交于点M,在线段PE上是否存一点N,使得△DMN与△DCO相似?若存在,试求出相应点的坐标;
③在①的条件下,点F是坐标轴上一点,且点F到EC、ED的距离相等,试直接写出EF的长度.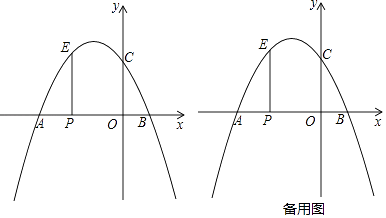
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com