
【题目】某股民上周五购进某公司股票500股,每股30元.(星期六、星期日封盘,关闭交易)下表是本周内每日该股票比前一天的涨跌情况(单位:元)

星期一,星期二被墨水污染,只知道星期一比上周五上涨10%,星期二比星期一下跌10%.根据以上信息,请回答:
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)已知该股民购进股票时付了1.5‰的手续费,卖出时还要付成交额1.5‰的手续费和1‰的交易税.如果他在星期五收盘时全部卖出该股票,他是赚钱还是亏本?赚或亏了多少钱?
【答案】(1)星期三收盘时,每股是31元;(2)本周内每股最高价是33元,最低价是29.7元;(3)他赚钱了,赚了937.5元.
【解析】
(1)根据题意即可求出。
(2)算出周一至周五每股的收盘价,进行比较得出即可。
(3)根据股票交易时的收益等于卖出的交易额减去卖出时的手续费成交额费,减去买进时的成本,买进时的手续费,可得答案.
(1)星期一收盘时: 30(1+10![]() )=33(元);
)=33(元);
星期二收盘时: 33(1-10![]() )=29.7(元);
)=29.7(元);
星期三收盘时:29.7+1.3=31(元).
答:星期三收盘时,每股是31元.
(2)星期一收盘时: 30(1+10![]() )=33(元);
)=33(元);
星期二收盘时: 30(1-10![]() )=29.7(元);
)=29.7(元);
星期三收盘时:29.7+1.3=31(元).
星期四收盘时:31-1=30(元);
星期五收盘时:30+2=32(元).
答:本周内每股最高价是33元,最低价是29.7元.
(3)投资+手续费= 500![]() (1+1.5‰)=15022.5(元);
(1+1.5‰)=15022.5(元);
卖出成交额-(手续费+交易税)=500![]() (1-1.5‰-1‰)=15960(元);
(1-1.5‰-1‰)=15960(元);
收益: 15960-15022.5=937.5(元).
答:他赚钱了,赚了937.5元.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD. 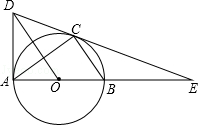
(1)求证:AD=CD;
(2)若DE是⊙O的切线,CD=3,CE=2,求tanE和cos∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(-2,0),B(0,6),C(6,0),∠ABC+∠ADC=180°,BC⊥CD.
(1)求证:∠ABO=∠CAD;
(2)求四边形ABCD的面积;
(3)如图2,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,已知AD=BC,AC=BD.求证:△ADB≌△BCA. 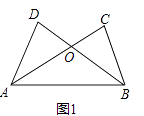
(2)如图2,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切于点D,若CD= ![]() ,求⊙O的半径.
,求⊙O的半径. 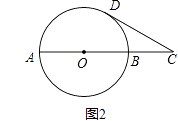
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.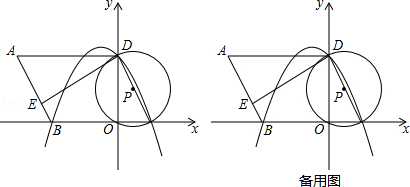
(1)求抛物线的解析式;
(2)说明ED是⊙P的切线,若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线上吗?请说明理由;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (x>0)交于点A,将直线y=
(x>0)交于点A,将直线y= ![]() x向下平移个6单位后,与双曲线y=
x向下平移个6单位后,与双曲线y= ![]() (x>0)交于点B,与x轴交于点C,则C点的坐标为;若
(x>0)交于点B,与x轴交于点C,则C点的坐标为;若 ![]() =2,则k= .
=2,则k= . 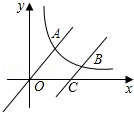
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长阳公园有四棵古树A,B,C,D (单位:米).
(1)请写出A,B,C,D四点的坐标;
(2)为了更好地保护古树,公园决定将如图所示的四边形EFGH用围栏圈起来,划为保护区,请你计算保护区的面积.
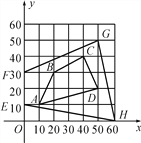
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com