
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹOÎȘÔ”ăŁŹÆœĐĐËıßĐÎABCD”ıßBCÔÚxÖáÉÏŁŹD”ăÔÚyÖáÉÏŁŹC”ăŚű±êÎȘŁš2ŁŹ0Ł©ŁŹBC=6ŁŹĄÏBCD=60ĄăŁŹ”ăEÊÇABÉÏÒ»”㣏AE=3EBŁŹĄŃPčęDŁŹOŁŹCÈę”㣏ƌÎïÏßy=ax2+bx+cčę”ăDŁŹBŁŹCÈę”㣟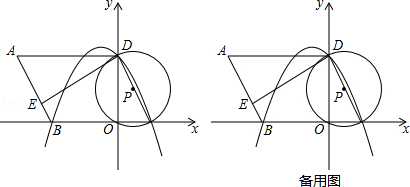
Łš1Ł©ÇóĆŚÎïÏߔĜâÎöÊœŁ»
Łš2Ł©Ë”ĂśEDÊÇĄŃP”ÄÇĐÏߣŹÈôœ«ĄśADEÈÆ”ăDÄæʱŐëĐęŚȘ90ĄăŁŹE”ă”ĶÔÓŠ”ăEĄä»áÂäÔÚĆŚÎïÏßÉÏÂđŁżÇë˔ÜÀíÓÉŁ»
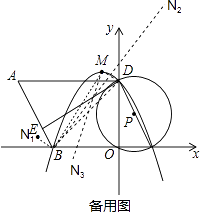
Łš3Ł©Èô”ăMÎȘŽËĆŚÎïÏߔĶ„”ăŁŹÆœĂæÉÏÊÇ·ńŽæÔÚ”ăNŁŹÊč”ĂÒÔ”ăBŁŹDŁŹMŁŹNÎȘ¶„”ă”ÄËıßĐÎÎȘÆœĐĐËıßĐÎŁżÈôŽæÔÚŁŹÇëÖ±œÓĐŽłö”ăN”ÄŚű±êŁ»ÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉŁź
ĄŸŽđ°žĄż
Łš1Ł©
œâŁșĄßC”ăŚű±êÎȘŁš2ŁŹ0Ł©ŁŹBC=6ŁŹ
ĄàBŁš©4ŁŹ0Ł©ŁŹ
ÔÚRtĄśOCDÖĐŁŹĄßtanĄÏOCD= ![]() ŁŹ
ŁŹ
ĄàOD=2tan60Ąă=2 ![]() ŁŹ
ŁŹ
ĄàDŁš0ŁŹ2 ![]() Ł©ŁŹ
Ł©ŁŹ
ÉèĆŚÎïÏߔĜâÎöÊœÎȘy=Łšx+4Ł©Łšx©2Ł©ŁŹ
°ŃDŁš0ŁŹ2 ![]() Ł©ŽúÈë”Ăa4Łš©2Ł©=2
Ł©ŽúÈë”Ăa4Łš©2Ł©=2 ![]() ŁŹ
ŁŹ
œâ”ĂŁșa=© ![]() ŁŹ
ŁŹ
ĄàĆŚÎïÏߔĜâÎöÊœÎȘy=© ![]() Łšx+4Ł©Łšx©2Ł©=©
Łšx+4Ł©Łšx©2Ł©=© ![]() x2©
x2© ![]() x+2
x+2 ![]()
Łš2Ł©
œâŁșÔÚRtĄśOCDÖĐŁŹCD=2OC=4ŁŹ
ĄßËıßĐÎABCDÊÇÆœĐĐËıßĐÎŁŹ
ĄàAB=CD=4ŁŹABĄÎCDŁŹĄÏA=ĄÏBCD=60ĄăŁŹAD=BC=6ŁŹ
ĄßAE=3BEŁŹ
ĄàAE=3ŁŹ
Ąà ![]() ŁŹ
ŁŹ ![]() =
= ![]() =
= ![]() ŁŹ
ŁŹ
Ąà ![]() ŁŹ
ŁŹ
ĄßĄÏDAE=ĄÏDCBŁŹ
ĄàĄśAEDĄŚĄśDCBŁŹ
ĄàĄÏADE=ĄÏCDOŁŹ
ĄßĄÏADE+ĄÏODE=90ĄăŁŹ
ĄàĄÏCDO+ĄÏODE=90ĄăŁŹ
ĄàCDĄÍDEŁŹ
ĄßĄÏDOC=90ĄăŁŹ
ĄàCDÎȘĄŃP”ÄÖ±Ÿ¶ŁŹ
ĄàEDÊÇĄŃP”ÄÇĐÏߣ»
E”ă”ĶÔÓŠ”ăEĄäČ»»áÂäÔÚĆŚÎïÏßÉÏŁŹ
ÀíÓÉŁșĄßĄśAEDĄŚĄśCODŁŹ
Ąà ![]() ŁŹ
ŁŹ
ŒŽ ![]() =
= ![]() ŁŹ
ŁŹ
œâ”ĂŁșDE=3 ![]() ŁŹ
ŁŹ
ĄßĄÏCDE=90ĄăŁŹDEŁŸDCŁŹ
Ąàœ«ĄśADEÈÆ”ăDÄæʱŐëĐęŚȘ90ĄăŁŹE”ă”ĶÔÓŠ”ăÔÚÉäÏßDCÉÏŁŹ¶ű”ăDŁŹCÔÚĆŚÎïÏßÉÏŁŹ
Ąà”ăEĄäČ»ÄÜÔÚĆŚÎïÏßÉÏ
Łš3Ł©
œâŁșŽæÔÚŁŹĄßy=© ![]() x2©
x2© ![]() x+2
x+2 ![]() =©
=© ![]() Łšx+1Ł©2+
Łšx+1Ł©2+ ![]() ŁŹ
ŁŹ
ĄàMŁš©1ŁŹ ![]() Ł©ŁŹ
Ł©ŁŹ
ĄßBŁš©4ŁŹ0Ł©ŁŹDŁš0ŁŹ2 ![]() Ł©ŁŹ
Ł©ŁŹ
ÈçÍŒŁŹ”±BMÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹ
”ăDÏòŚóÆœÒÆ4žö”„λŁŹÔÙÏòÏÂÆœÒÆ2 ![]() žö”„λ”Ă”œBŁŹ
žö”„λ”Ă”œBŁŹ
Ôò”ăMŁš©1ŁŹ ![]() Ł©ÏòŚóÆœÒÆ4žö”„λŁŹÔÙÏòÏÂÆœÒÆ2
Ł©ÏòŚóÆœÒÆ4žö”„λŁŹÔÙÏòÏÂÆœÒÆ2 ![]() žö”„λ”Ă”œN1Łš©5ŁŹ
žö”„λ”Ă”œN1Łš©5ŁŹ ![]() Ł©Ł»
Ł©Ł»
”±DMÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹ
”ăBÏòÓÒÆœÒÆ3žö”„λŁŹÔÙÏòÉÏÆœÒÆ ![]() žö”„λ”Ă”œDŁŹ
žö”„λ”Ă”œDŁŹ
Ôò”ăMŁš©1ŁŹ ![]() Ł©ÏòÓÒÆœÒÆ4žö”„λŁŹÔÙÏòÉÏÆœÒÆ2
Ł©ÏòÓÒÆœÒÆ4žö”„λŁŹÔÙÏòÉÏÆœÒÆ2 ![]() žö”„λ”Ă”œN2Łš3ŁŹ
žö”„λ”Ă”œN2Łš3ŁŹ ![]() Ł©Ł»
Ł©Ł»
”±BDÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹ
”ăMÏòÓÒÆœÒÆ1žö”„λŁŹÔÙÏòÏÂÆœÒÆ ![]() žö”„λ”Ă”œDŁŹ
žö”„λ”Ă”œDŁŹ
Ôò”ăBŁš©4ŁŹ0Ł©ÏòÓÒÆœÒÆ1žö”„λŁŹÔÙÏòÏÂÆœÒÆ ![]() žö”„λ”Ă”œN3Łš©3ŁŹ©
žö”„λ”Ă”œN3Łš©3ŁŹ© ![]() Ł©Ł»
Ł©Ł»
ŚÛÉÏËùÊöŁŹÒÔ”ăBŁŹDŁŹMŁŹNÎȘ¶„”ă”ÄËıßĐÎÎȘÆœĐĐËıßĐÎʱŁŹ”ăN”ÄŚű±êÎȘŁš©5ŁŹ ![]() Ł©»òŁš3ŁŹ
Ł©»òŁš3ŁŹ ![]() Ł©»òŁš©3ŁŹ©
Ł©»òŁš©3ŁŹ© ![]() Ł©Łź
Ł©Łź
ĄŸœâÎöĄżŁš1Ł©œâÖ±œÇÈęœÇĐΔÔœDŁš0ŁŹ2 ![]() Ł©ŁŹÉèĆŚÎïÏߔĜâÎöÊœÎȘy=Łšx+4Ł©Łšx©2Ł©ŁŹ°ŃDŁš0ŁŹ2
Ł©ŁŹÉèĆŚÎïÏߔĜâÎöÊœÎȘy=Łšx+4Ł©Łšx©2Ł©ŁŹ°ŃDŁš0ŁŹ2 ![]() Ł©ŒŽżÉ”Ă”œœáÂÛŁ»Łš2Ł©žùŸĘÆœĐĐËıßĐΔÄĐÔÖÊ”Ă”œAB=CD=4ŁŹABĄÎCDŁŹĄÏA=ĄÏBCD=60ĄăŁŹAD=BC=6ŁŹžùŸĘÏàËÆÈęœÇĐΔÄĐÔÖÊ”Ă”œĄÏADE=ĄÏCDOŁŹÓÚÊǔÔœCDÎȘĄŃP”ÄÖ±Ÿ¶ŁŹžùŸĘÇĐÏß”ÄĆжš¶šÀí”Ă”œEDÊÇĄŃP”ÄÇĐÏߣ»E”ă”ĶÔÓŠ”ăEĄäČ»»áÂäÔÚĆŚÎïÏßÉÏŁŹžùŸĘÏàËÆÈęœÇĐΔÄÏëÖȘ”À”ÄDE=3
Ł©ŒŽżÉ”Ă”œœáÂÛŁ»Łš2Ł©žùŸĘÆœĐĐËıßĐΔÄĐÔÖÊ”Ă”œAB=CD=4ŁŹABĄÎCDŁŹĄÏA=ĄÏBCD=60ĄăŁŹAD=BC=6ŁŹžùŸĘÏàËÆÈęœÇĐΔÄĐÔÖÊ”Ă”œĄÏADE=ĄÏCDOŁŹÓÚÊǔÔœCDÎȘĄŃP”ÄÖ±Ÿ¶ŁŹžùŸĘÇĐÏß”ÄĆжš¶šÀí”Ă”œEDÊÇĄŃP”ÄÇĐÏߣ»E”ă”ĶÔÓŠ”ăEĄäČ»»áÂäÔÚĆŚÎïÏßÉÏŁŹžùŸĘÏàËÆÈęœÇĐΔÄÏëÖȘ”À”ÄDE=3 ![]() ŁŹžùŸĘĐęŚȘ”ÄÏëÖȘ”À”ÄE”ă”ĶÔÓŠ”ăÔÚÉäÏßDCÉÏŁŹ¶ű”ăDŁŹCÔÚĆŚÎïÏßÉÏŁŹÓÚÊǔÔœ”ăEĄäČ»ÄÜÔÚĆŚÎïÏßÉÏŁ»Łš3Ł©žùŸĘ¶țŽÎșŻÊę”ÄœâÎöÊœ”Ă”œMŁš©1ŁŹ
ŁŹžùŸĘĐęŚȘ”ÄÏëÖȘ”À”ÄE”ă”ĶÔÓŠ”ăÔÚÉäÏßDCÉÏŁŹ¶ű”ăDŁŹCÔÚĆŚÎïÏßÉÏŁŹÓÚÊǔÔœ”ăEĄäČ»ÄÜÔÚĆŚÎïÏßÉÏŁ»Łš3Ł©žùŸĘ¶țŽÎșŻÊę”ÄœâÎöÊœ”Ă”œMŁš©1ŁŹ ![]() Ł©ŁŹÓÉBŁš©4ŁŹ0Ł©ŁŹDŁš0ŁŹ2
Ł©ŁŹÓÉBŁš©4ŁŹ0Ł©ŁŹDŁš0ŁŹ2 ![]() Ł©ŁŹ”±BMÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹ”±DMÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹ”±BDÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹžùŸĘÆœÒÆ”ÄĐÔÖÊŒŽżÉ”Ă”œœáÂÛŁź
Ł©ŁŹ”±BMÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹ”±DMÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹ”±BDÎȘÆœĐĐËıßĐÎBDMN”ĶԜÇÏßʱŁŹžùŸĘÆœÒÆ”ÄĐÔÖÊŒŽżÉ”Ă”œœáÂÛŁź
ĄŸżŒ”ăŸ«ÎöĄżŐÆÎŐÆœĐĐËıßĐΔÄĐÔÖÊșÍœâÖ±œÇÈęœÇĐÎÊÇœâŽđ±ŸÌâ”Äžù±ŸŁŹĐèÒȘÖȘ”ÀÆœĐĐËıßĐΔĶԱßÏà”ÈÇÒÆœĐĐŁ»ÆœĐĐËıßĐΔĶԜÇÏà”ÈŁŹÁڜǻ„ČčŁ»ÆœĐĐËıßĐΔĶԜÇÏß»„ÏàÆœ·ÖŁ»œâÖ±œÇÈęœÇĐΔÄÒÀŸĘŁșąÙ±ß”ÄčŰÏ”a2+b2=c2Ł»ąÚœÇ”ÄčŰÏ”ŁșA+B=90ĄăŁ»ąÛ±ßœÇčŰÏ”ŁșÈęœÇșŻÊę”ĶšÒ棟(ŚąÒâŁșŸĄÁż±ÜĂâÊčÓĂÖĐŒäÊęŸĘșÍłę·š)Łź


 Ò»±ŸșĂÌâżÚËăÌâżšÏ”ÁĐŽđ°ž
Ò»±ŸșĂÌâżÚËăÌâżšÏ”ÁĐŽđ°ž
| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżĐĄÇżÊÇУѧÉú»áÌćÓęȿȿł€ŁŹËûÏëÁËœâÏÖÔÚ͏ѧĂÇžüÏČ»¶ÊČĂŽÇòÀàÔ˶ŻŁŹÒÔ±ăѧÉú»áŚéÖŻÊÜ»¶Ó”ıÈÈü.ÓÚÊÇËûÉèŒÆÁË”śČéÎÊŸíŁŹÔÚÈ«ĐŁĂżžö°à¶ŒËæ»úŃĄÈĄÁËÒ»¶šÊęÁż”ÄѧÉúœűĐĐ”śČ飏”śČéÎÊŸíÈçÏÂŁș
”śČéÎÊŸí
ÄăŚîÏČ»¶”ÄÇòÀàÔ˶ŻÊÇŁš Ł©Łš”„ŃĄŁ©
AĄąÀșÇòBĄąŚăÇòCĄąĆĆÇòDĄąÆčĆÒÇòEĄąÓđĂ«ÇòFĄąÆäËû
”śČéÎÊŸí
ÄăŚîÏČ»¶”ÄÇòÀàÔ˶ŻÊÇŁš Ł©Łš”„ŃĄŁ©
AĄąÀșÇòBĄąŚăÇòCĄąĆĆÇòDĄąÆčĆÒÇòEĄąÓđĂ«ÇòFĄąÆäËû
ĐĄÇżžùŸĘÍłŒÆÊęŸĘÖÆŚś”Äžś»î¶ŻĐĄŚéÈËÊę·ÖČŒÇéżö”ÄÍłŒÆ±íșÍÉÈĐÎÍłŒÆÍŒÈçÏÂ
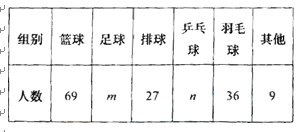

Łš1Ł©ÇëÄăĐŽłöÍłŒÆ±íÖĐżŐÈ±Čż·Ö”ÄÈËÊęm= , n= .
Łš2Ł©ÔÚÉÈĐÎÍłŒÆÍŒÖĐŁŹÓđĂ«ÇòËù¶ÔÓŠ”ÄÉÈĐÎÔČĐĜǔÈÓÚ .
Łš3Ł©ÇëÄăžùŸĘ”śČéœáčûŁŹžűХǿȿł€ŒòÒȘÌáłöÁœÌőșÏÀí»Ż”ÄœšÒ食
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÏÂÁĐË”·šŐęÈ·”ÄÊÇŁš Ł©
A.ÖÀÒ»Ă¶ÖÊ”ŰŸùÔÈ”ÄŐę·œÌćś»ŚÓŁŹś»ŚÓÍŁÖčŚȘ¶ŻșóŁŹ5”㳯ÉÏÊDZŰÈ»ÊÂŒț
B.ÉóČéÊéžćÖĐÓĐÄÄЩѧżÆĐÔŽíÎóÊÊșÏÓĂłéŃù”śČé·š
C.ŒŚÒÒÁœÈËÔÚÏàÍŹÌőŒțÏžśÉ仜10ŽÎŁŹËûĂÇ”ÄłÉŒš”ÄÆœŸùÊęÏàÍŹŁŹ·œČî·Ö±đÊÇSŒŚ2=0.4ŁŹSÒÒ2=0.6ŁŹÔòŒŚ”ÄÉ仜łÉŒšœÏÎȶš
D.ÖÀÁœĂ¶ÖÊ”ŰŸùÔÈ”ÄÓČ±ÒŁŹĄ°ÁœĂ¶ÓČ±Ò¶ŒÊÇŐęĂæłŻÉÏĄ±ŐâÒ»ÊÂŒț·ąÉú”ÄžĆÂÊÎȘ ![]()
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
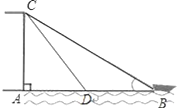
ĄŸÌâÄżĄżÒŃÖȘŁșÈçÍŒŁŹÓĐÈËÔÚ°¶ÉÏ”ăC”Ĕ۷œŁŹÓĂÉțŚÓÀŽŹżż°¶ŁŹżȘʌʱŁŹÉțł€CB=10ĂŚŁŹCAĄÍABŁŹÇÒCA=6ĂŚŁŹÀ¶ŻÉțŚÓœ«ŽŹŽÓ”ăBŃŰBA·œÏòĐĐÊ»”œ”ăDșóŁŹÉțł€CD=6![]() ĂŚŁź
ĂŚŁź
Łš1Ł©ÊÔĆжšĄśACD”ÄĐÎŚŽŁŹČąË”ĂśÀíÓÉŁ»
Łš2Ł©ÇóŽŹÌćÒƶŻŸàÀëBD”Äł€¶ÈŁź

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÄłčÉĂńÉÏÖÜÎćčșœűÄłč«ËŸčÉƱ500čÉŁŹĂżčÉ30ÔȘŁźŁšĐÇÆÚÁùĄąĐÇÆÚÈŐ·âĆÌŁŹčŰ±Őœ»ÒŚŁ©Ï±íÊDZŸÖÜÄÚĂżÈŐžĂčÉƱ±ÈÇ°Ò»Ìì”ÄŐÇ”űÇéżöŁš”„λŁșÔȘŁ©

ĐÇÆÚÒ»ŁŹĐÇÆÚ¶ț±»Ä«ËźÎÛÈŸŁŹÖ»ÖȘ”ÀĐÇÆÚÒ»±ÈÉÏÖÜÎćÉÏŐÇ10%ŁŹĐÇÆÚ¶ț±ÈĐÇÆÚһϔű10%ŁźžùŸĘÒÔÉÏĐĆÏąŁŹÇë»ŰŽđŁș
Łš1Ł©ĐÇÆÚÈęÊŐĆÌʱŁŹĂżčÉÊǶàÉÙÔȘ?
Łš2Ł©±ŸÖÜÄÚĂżčÉŚîžßŒÛÊǶàÉÙÔȘŁżŚî”ÍŒÛÊǶàÉÙÔȘŁż
Łš3Ł©ÒŃÖȘžĂčÉĂńčșœűčÉƱʱž¶ÁË1.5Ąë”ÄÊÖĐű·ŃŁŹÂôłöʱ»čÒȘž¶łÉœ»¶î1.5Ąë”ÄÊÖĐű·ŃșÍ1Ąë”Äœ»ÒŚË°ŁźÈçčûËûÔÚĐÇÆÚÎćÊŐĆÌÊ±È«ČżÂôłöžĂčÉƱŁŹËûÊÇŚŹÇź»čÊÇżś±ŸŁżŚŹ»òżśÁ˶àÉÙÇźŁż
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘÁËœâѧÉúżÎÍâÔĶÁ”ÄÏČșĂŁŹÄłĐŁŽÓ°ËÄꌶËæ»úłéÈĄČż·ÖѧÉúœűĐĐÎÊŸí”śČ飏”śČéÒȘÇóĂżÈËÖ»ŃĄÈĄÒ»ÖÖÏČ»¶”ÄÊéŒźŁŹÈçčûĂ»ÓĐÏČ»¶”ÄÊéŒźŁŹÔòŚśĄ°ÆäËüĄ±ÀàÍłŒÆĄŁÍŒŁš1Ł©ÓëÍŒŁš2Ł©ÊÇŐûÀíÊęŸĘșó»æÖÆ”ÄÁœ·ùČ»ÍêŐû”ÄÍłŒÆÍŒĄŁÒÔÏÂœáÂÛČ»ŐęÈ·”ÄÊÇŁš Ł©
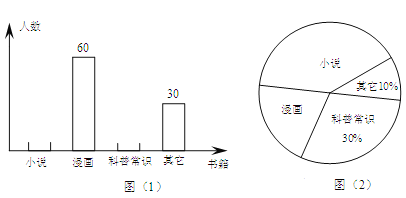
A. ÓÉŐâÁœžöÍłŒÆÍŒżÉÖȘÏČ»¶Ą°żÆÆŐłŁÊ¶Ą±”ÄѧÉúÓĐ90ÈËŁź
B. ÈôžĂÄꌶčČÓĐ1200ĂûѧÉúŁŹÔòÓÉŐâÁœžöÍłŒÆÍŒżÉčÀŒÆÏČ°źĄ°żÆÆŐłŁÊ¶Ą±”ÄѧÉúÔŒÓĐ360žöŁź
C. ÓÉŐâÁœžöÍłŒÆÍŒČ»ÄÜÈ·¶šÏČ»¶Ą°ĐĄË”Ą±”ÄÈËÊ꣟
D. ÔÚÉÈĐÎÍłŒÆÍŒÖĐŁŹĄ°Âț»Ą±ËùÔÚÉÈĐΔÄÔČĐÄœÇÎȘ72ĄăŁź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÎȘÁ˱Ł»€»·Ÿł,ijУ»·±ŁĐĄŚéłÉԱХÜÊŐŒŻ·Ï”çłŰ,”ÚÒ»ÌìÊŐŒŻ1șĆ”çłŰ4œÚ,5șĆ”çłŰ5œÚ,ŚÜÖÊÁżÎȘ450żË;”Ú¶țÌìÊŐŒŻ1șĆ”çłŰ2œÚ,5șĆ”çłŰ3œÚ,ŚÜÖÊÁżÎȘ240żË.
(1)Çó1șĆ”çłŰșÍ5șĆ”çłŰĂżœÚ·Ö±đÖ۶àÉÙżË;
(2)ѧУ»·±ŁĐĄŚéÎȘčÀËăËÄÔ·ĘÊŐŒŻ·Ï”çłŰ”ÄŚÜÖÊÁż,ËûĂÇËæ»úłéÈĄÁËžĂÔÂÄł5ÌìĂżÌìÊŐŒŻ·Ï”çłŰ”ÄÊęÁż,Èçϱí:
1șĆ·Ï”çłŰÊęÁż/œÚ | 29 | 30 | 32 | 28 | 31 |
5șĆ·Ï”çłŰÊęÁż/œÚ | 51 | 53 | 47 | 49 | 50 |
·Ö±đŒÆËăÊŐŒŻ”ÄÁœÖÖ·Ï”çłŰÊęÁż”ÄŃù±ŸÆœŸùÊę,ČąÓÉŽËčÀËăžĂÔ»·±ŁĐĄŚéÊŐŒŻ·Ï”çłŰ”ÄŚÜÖÊÁżÊǶàÉÙǧżË;
(3)ÊÔ˔ÜÉÏÊö±ížńÖĐÊęŸĘ”Ä»ńÈĄ·œ·šÊÇłéŃù”śČé»čÊÇÈ«Ăæ”śČé,ÄăÈÏÎȘŐâÖÖ·œ·šșÏÀíÂđ?
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄż¶țŽÎșŻÊęy=ax2+bx+c”ÄÍŒÏóÈçÍŒËùÊŸŁŹ¶ÔłÆÖáÊÇx=©1ŁŹÏÂÁĐœáÂÛŁșŁš1Ł©acŁŒ0Ł»Łš2Ł©4acŁŒb2Ł»Łš3Ł©2a+b=0Ł»Łš4Ł©a©b+cŁŸ2ŁŹÆäÖĐŐęÈ·”ÄœáÂÛčČÓĐŁš Ł© 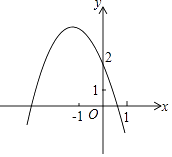
A.1žö
B.2žö
C.3žö
D.4žö
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÌœËśčéÄÉŁș
Łš1Ł©ÈçÍŒ1ŁŹÒŃÖȘĄśABCÎȘÖ±œÇÈęœÇĐÎŁŹĄÏA=90ĄăŁŹÈôŃŰÍŒÖĐĐéÏߌôÈ„ĄÏAŁŹ ÔòĄÏ1+ĄÏ2”ÈÓÚ
A.90Ąă B.135Ąă C.270Ąă D.315Ąă
Łš2Ł©ÈçÍŒ2ŁŹÒŃÖȘĄśABCÖĐŁŹĄÏA=40ĄăŁŹŒôÈ„ĄÏAșółÉËıßĐÎŁŹÔòĄÏ1+ĄÏ2=
Łš3Ł©ÈçÍŒ2ŁŹžùŸĘŁš1Ł©Ó룚2Ł©”ÄÇóœâčęłÌŁŹÇëÄăčéÄÉČÂÏëĄÏ1+ĄÏ2ÓëĄÏA”ÄčŰÏ”ÊÇ
Łš4Ł©ÈçÍŒ3ŁŹÈôĂ»ÓĐŒô”ôŁŹ¶űÊÇ°ŃËüŐÛłÉÈçÍŒ3ĐÎŚŽŁŹÊÔÌœŸżĄÏ1+ĄÏ2ÓëĄÏA”ÄčŰÏ”ČąË”ĂśÀíÓÉŁź

Č鿎Žđ°žșÍœâÎö>>
čúŒÊѧУÓĆŃĄ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com