
【题目】为了保护环境,某校环保小组成员小明收集废电池,第一天收集1号电池4节,5号电池5节,总质量为450克;第二天收集1号电池2节,5号电池3节,总质量为240克.
(1)求1号电池和5号电池每节分别重多少克;
(2)学校环保小组为估算四月份收集废电池的总质量,他们随机抽取了该月某5天每天收集废电池的数量,如下表:
1号废电池数量/节 | 29 | 30 | 32 | 28 | 31 |
5号废电池数量/节 | 51 | 53 | 47 | 49 | 50 |
分别计算收集的两种废电池数量的样本平均数,并由此估算该月环保小组收集废电池的总质量是多少千克;
(3)试说明上述表格中数据的获取方法是抽样调查还是全面调查,你认为这种方法合理吗?
【答案】(1)75克,30克 (2)30节,50节,112.5千克 (3)抽样调查,合理
【解析】
(1)根据题意,设出两个未知数,利用方程组对题目进行求解,列出方程的关键在于找出等量关系式,题目中存在两个等量关系;
(2)可以利用平均数的定义求出每天所收集两种电池的数量,进而可以求出四月所收集电池总量,此时即可求出所收集电池的总质量;
(3)根据抽样调查的特点进行判断即可.
(1)设1号电池每节的质量为x克,5号电池每节的质量为y克.
依题意,得![]() 解得
解得![]()
答:1号电池每节的质量为75克,5号电池每节的质量为30克.
(2)收集1号废电池数量的样本平均数为![]() =30(节).
=30(节).
收集5号废电池数量的样本平均数为![]() =50(节).
=50(节).
所以每天可收集的废电池总质量为30×75+50×30=3750(克),因而估算该月环保小组收集废电池的总质量是3750×30=112500(克)=112.5(千克).
(3)表格中的数据是抽样调查的结果,合理,抽样时保证了样本的“随机性”.
故答案为:(1)75克,30克 (2)30节,50节,112.5千克 (3)抽样调查,合理.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,A(-2,0),B(0,6),C(6,0),∠ABC+∠ADC=180°,BC⊥CD.
(1)求证:∠ABO=∠CAD;
(2)求四边形ABCD的面积;
(3)如图2,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,O为原点,平行四边形ABCD的边BC在x轴上,D点在y轴上,C点坐标为(2,0),BC=6,∠BCD=60°,点E是AB上一点,AE=3EB,⊙P过D,O,C三点,抛物线y=ax2+bx+c过点D,B,C三点.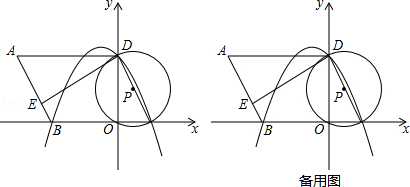
(1)求抛物线的解析式;
(2)说明ED是⊙P的切线,若将△ADE绕点D逆时针旋转90°,E点的对应点E′会落在抛物线上吗?请说明理由;
(3)若点M为此抛物线的顶点,平面上是否存在点N,使得以点B,D,M,N为顶点的四边形为平行四边形?若存在,请直接写出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (x>0)交于点A,将直线y=
(x>0)交于点A,将直线y= ![]() x向下平移个6单位后,与双曲线y=
x向下平移个6单位后,与双曲线y= ![]() (x>0)交于点B,与x轴交于点C,则C点的坐标为;若
(x>0)交于点B,与x轴交于点C,则C点的坐标为;若 ![]() =2,则k= .
=2,则k= . 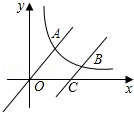
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=∠2,那么添加一个条件后,仍无法判定△ABD≌△ACD的是( )
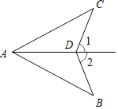
A. AB=AC B. ∠B=∠C C. AD平分∠CAB D. CD=BD
查看答案和解析>>
科目:初中数学 来源: 题型:
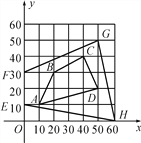
【题目】长阳公园有四棵古树A,B,C,D (单位:米).
(1)请写出A,B,C,D四点的坐标;
(2)为了更好地保护古树,公园决定将如图所示的四边形EFGH用围栏圈起来,划为保护区,请你计算保护区的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为 .
(k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为 . 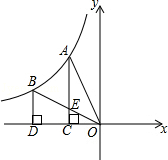
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,BC=5,过点A作AE⊥AB且AB=AE,过点E分别作EF⊥AC,ED⊥BC,分别交AC和BC的延长线与点F、D.
(1)求证:△ABC≌△EAF;
(2)若FC=7,求四边形ABDE的周长.
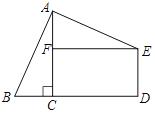
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com