
【题目】如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD. 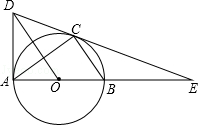
(1)求证:AD=CD;
(2)若DE是⊙O的切线,CD=3,CE=2,求tanE和cos∠ABC的值.
【答案】
(1)证明:∵AB为直径,
∴∠ACB=90°,
∴BC⊥AC,
∵OD∥BC,
∴OD⊥AC,
∴OD平分AC,即OD垂直平分AC,
∴AD=CD
(2)解:连结OC,如图,设⊙O的半径为r,
∵BC∥OD,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,解得BE=
,解得BE= ![]() r,
r,
∵DE为切线,
∴OC⊥DE,
∴∠OCD=∠OCE=90°,
在△OAD和△OCD中,
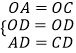 ,
,
∴△OAD≌△OCD,
∴∠OAD=90°,
在Rt△ADE中,∵AD=AC=3,DE=DC+CE=5,
∴AE= ![]() =4,
=4,
∴tanE= ![]() =
= ![]() ,
,
∵OD∥BC,
∴∠ABC=∠AOD,
在Rt△AOD中,OD= ![]() =
= ![]() =
= ![]() ,
,
∴cos∠AOD= ![]() =
= ![]() =
= ![]() ,
,
∴cos∠ABC= ![]()
答:tanE= ![]() ,cos∠ABC=
,cos∠ABC= ![]() .
.
【解析】(1)先利用圆周角定理得到∠ACB=90°,再利用OD∥BC得到OD⊥AC,然后根据垂径定理和线段垂直平分线的性质可得到结论; 2)连结OC,如图,设⊙O的半径为r,先利用平行线分线段成比例定理得到r= ![]() ,再证明△OAD≌△OCD得到∠OAD=90°,则根据勾股定理可计算出AE=4,这样利用正切定理可得tanE的值,再利用OD∥BC得到∠ABC=∠AOD,然后在Rt△AOD中,先计算出OD,再利用余弦得到cos∠AOD的值,从而得到cos∠ABC的值.
,再证明△OAD≌△OCD得到∠OAD=90°,则根据勾股定理可计算出AE=4,这样利用正切定理可得tanE的值,再利用OD∥BC得到∠ABC=∠AOD,然后在Rt△AOD中,先计算出OD,再利用余弦得到cos∠AOD的值,从而得到cos∠ABC的值.
【考点精析】解答此题的关键在于理解三角形的外接圆与外心的相关知识,掌握过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,AC=BC,点E是AC上一点,连接BE. 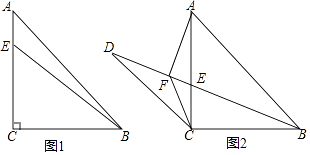
(1)如图1,若AB=4 ![]() ,BE=5,求AE的长;
,BE=5,求AE的长;
(2)如图2,点D是线段BE延长线上一点,过点A作AF⊥BD于点F,连接CD、CF,当AF=DF时,求证:DC=BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y= ![]() (x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )
(x>0)的图象与边长是6的正方形OABC的两边AB,BC分别相交于M,N 两点,△OMN的面积为10.若动点P在x轴上,则PM+PN的最小值是( )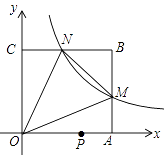
A.6 ![]()
B.10
C.2 ![]()
D.2 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向下平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
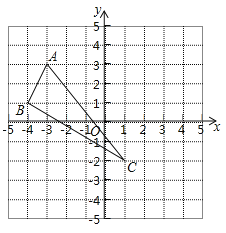
(2)直接写出A′、B′、C′三点的坐标:
A′(_____,______); B′(_____,______);
C′(_____,______).
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
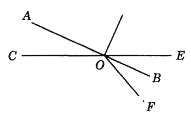
【题目】如图所示,直线AB、CE交于O,
(1)写出∠AOC的对顶角和邻补角;
(2)写出∠COF的邻补角;
(3)写出∠BOF的邻补角;
(4)写出∠AOE的对顶角及其所有的邻补角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件
B.审查书稿中有哪些学科性错误适合用抽样调查法
C.甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定
D.掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某股民上周五购进某公司股票500股,每股30元.(星期六、星期日封盘,关闭交易)下表是本周内每日该股票比前一天的涨跌情况(单位:元)

星期一,星期二被墨水污染,只知道星期一比上周五上涨10%,星期二比星期一下跌10%.根据以上信息,请回答:
(1)星期三收盘时,每股是多少元?
(2)本周内每股最高价是多少元?最低价是多少元?
(3)已知该股民购进股票时付了1.5‰的手续费,卖出时还要付成交额1.5‰的手续费和1‰的交易税.如果他在星期五收盘时全部卖出该股票,他是赚钱还是亏本?赚或亏了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
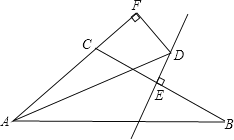
【题目】已知:如图,△ABC中,∠A的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF垂直于AC交AC的延长线于点F.求证:AB﹣AC=2CF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com