
【题目】如图所示,直线AB、CE交于O,
(1)写出∠AOC的对顶角和邻补角;
(2)写出∠COF的邻补角;
(3)写出∠BOF的邻补角;
(4)写出∠AOE的对顶角及其所有的邻补角.
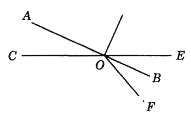
【答案】(1)∠AOC的对顶角是∠BOE,邻补角是∠BOC,∠AOE;
(2)∠COF的邻补角是∠EOF;
(3)∠BOF的邻补角是∠AOF;
(4)∠AOE的对顶角∠BOC,邻补角是∠AOC,∠BOE.
【解析】(1)(4)根据对顶角的定义、邻补角的定义找出即可;
(2)(3)根据邻补角的定义找出即可.
解:(1)∠AOC的对顶角是∠BOE,邻补角是∠BOC,∠AOE;
(2)∠COF的邻补角是∠EOF;
(3)∠BOF的邻补角是∠AOF;
(4)∠AOE的对顶角∠BOC,邻补角是∠AOC,∠BOE.
“点睛”本题考查了对顶角和邻补角的定义,熟记概念并准确识图是解题的关键,要注意一个角的邻补角有两个.


科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“数形结合"是一种重要的数学思想,观察下面的图形和算式.
![]()
![]()
![]()
![]()
解答下列问题:
(1)试猜想1+3+5+7+9+…+19=______=( );
(2)试猜想,当n是正整数时,1+3+5+7+9+…+(2n-1)= ;
(3)请用(2)中得到的规律计算:19+21+23+25+27+…+99.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为响应珠海环保城市建设,我市某污水处理公司不断改进污水处理设备,新设备每小时处理污水量是原系统的1.5倍,原来处理1200m3污水所用的时间比现在多用10小时.
(1)原来每小时处理污水量是多少m2?
(2)若用新设备处理污水960m3,需要多长时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC的中点,点E、F分别在线段AD及其延长线上,且DE=DF.下列条件使四边形BECF为菱形的是( ) 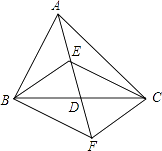
A.BE⊥CE
B.BF∥CE
C.BE=CF
D.AB=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD. 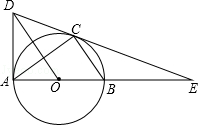
(1)求证:AD=CD;
(2)若DE是⊙O的切线,CD=3,CE=2,求tanE和cos∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
(1)求证:EM∥NG;
(2)连接EG,在GN上取一点H,使∠HEG=∠HGE,作∠FEH的平分线EP交AB于点P,求∠PEG的度数.
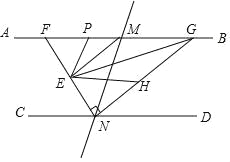
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合题。
(1)如图1,已知AD=BC,AC=BD.求证:△ADB≌△BCA. 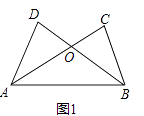
(2)如图2,已知AB是⊙O的一条直径,延长AB至点C,使AC=3BC,CD与⊙O相切于点D,若CD= ![]() ,求⊙O的半径.
,求⊙O的半径. 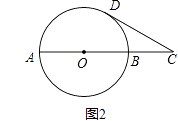
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com