
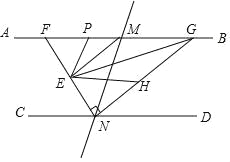
【题目】如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
(1)求证:EM∥NG;
(2)连接EG,在GN上取一点H,使∠HEG=∠HGE,作∠FEH的平分线EP交AB于点P,求∠PEG的度数.
【答案】(1)证明见解析;(2)45°.
【解析】
(1)根据平行线的性质以及角平分线得到定义,即可得出∠MEN=90°,再根据NG⊥EN,即可得到∠MEN+∠ENH=180°,进而得到EM∥NG;
(2)先设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°-2x,根据EP平分∠FEH,可得∠FEH=2(∠PEG+x),再根据∠FEH+∠HEN=180°,可得方程2(∠PEG+x)+90°-2x=180°,进而解得∠PEG.
解:(1)∵AB∥CD,
∴∠AMN+∠CNM=180°,
∵ME,NE分别是∠AMN与∠CNM的平分线,
∴∠EMN=![]() ∠AMN,∠ENM=
∠AMN,∠ENM=![]() ∠MNC,
∠MNC,
∴∠EMN+∠ENM=90°,即∠MEN=90°,
又∵NG⊥EN,
∴∠MEN+∠ENH=180°,
∴EM∥NG;
(2)设∠HEG=x,则∠HGE=∠MEG=x,∠NEH=90°﹣2x,
∵EP平分∠FEH,
∴∠FEH=2∠PEH=2(∠PEG+x),
又∵∠FEH+∠HEN=180°,
∴2(∠PEG+x)+90°﹣2x=180°,
解得∠PEG=45°.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.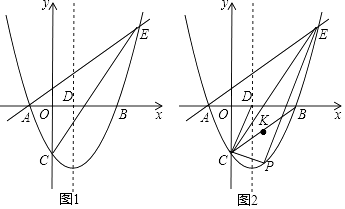
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
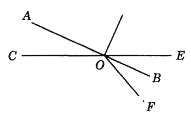
【题目】如图所示,直线AB、CE交于O,
(1)写出∠AOC的对顶角和邻补角;
(2)写出∠COF的邻补角;
(3)写出∠BOF的邻补角;
(4)写出∠AOE的对顶角及其所有的邻补角.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠A+∠D=180°,∠1=3∠2,∠2=24°,点P是BC上的一点.
(1)请写出图中∠1的一对同位角,一对内错角,一对同旁内角;
(2)求∠EFC与∠E的度数;
(3)若∠BFP=46°,请判断CE与PF是否平行?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.
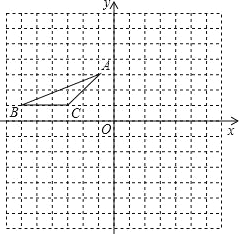
(1)按要求作图:
①△ABC关于x轴对称的图形△A1B1C1;
②将△A1B1C1向右平移7个单位得到△A2B2C2.
(2)回答下列问题:
①△A2B2C2中顶点B2坐标为 .
②若P(a,b)为△ABC边上一点,则按照(1)中①、②作图,点P对应的点P2的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
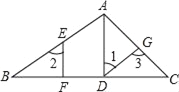
【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com