
【题目】如图,在平面直角坐标系中,抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.
与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,对称轴与x轴交于点D,点E(4,n)在抛物线上.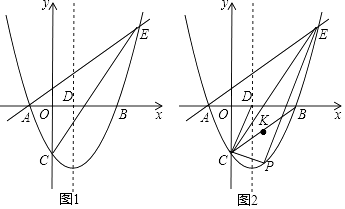
(1)求直线AE的解析式;
(2)点P为直线CE下方抛物线上的一点,连接PC,PE.当△PCE的面积最大时,连接CD,CB,点K是线段CB的中点,点M是CP上的一点,点N是CD上的一点,求KM+MN+NK的最小值;
(3)点G是线段CE的中点,将抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() 沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
沿x轴正方向平移得到新抛物线y′,y′经过点D,y′的顶点为点F.在新抛物线y′的对称轴上,是否存在一点Q,使得△FGQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
【答案】
(1)
解:∵y= ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ,
,
∴y= ![]() (x+1)(x﹣3).
(x+1)(x﹣3).
∴A(﹣1,0),B(3,0).
当x=4时,y= ![]() .
.
∴E(4, ![]() ).
).
设直线AE的解析式为y=kx+b,将点A和点E的坐标代入得: 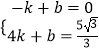 ,
,
解得:k= ![]() ,b=
,b= ![]() .
.
∴直线AE的解析式为y= ![]() x+
x+ ![]() .
.
(2)
解:设直线CE的解析式为y=mx﹣ ![]() ,将点E的坐标代入得:4m﹣
,将点E的坐标代入得:4m﹣ ![]() =
= ![]() ,解得:m=
,解得:m= ![]() .
.
∴直线CE的解析式为y= ![]() x﹣
x﹣ ![]() .
.
过点P作PF∥y轴,交CE与点F.
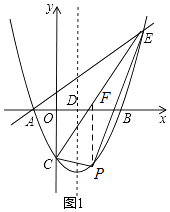
设点P的坐标为(x, ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ),则点F(x,
),则点F(x, ![]() x﹣
x﹣ ![]() ),
),
则FP=( ![]() x﹣
x﹣ ![]() )﹣(
)﹣( ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() )=
)= ![]() x2+
x2+ ![]() x.
x.
∴△EPC的面积= ![]() ×(
×( ![]() x2+
x2+ ![]() x)×4=﹣
x)×4=﹣ ![]() x2+
x2+ ![]() x.
x.
∴当x=2时,△EPC的面积最大.
∴P(2,﹣ ![]() ).
).
如图2所示:作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.
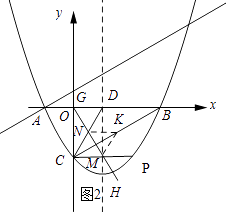
∵K是CB的中点,
∴k( ![]() ,﹣
,﹣ ![]() ).
).
∵点H与点K关于CP对称,
∴点H的坐标为( ![]() ,﹣
,﹣ ![]() ).
).
∵点G与点K关于CD对称,
∴点G(0,0).
∴KM+MN+NK=MH+MN+GN.
当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH.
∴GH= ![]() =3.
=3.
∴KM+MN+NK的最小值为3.
(3)
解:如图3所示:
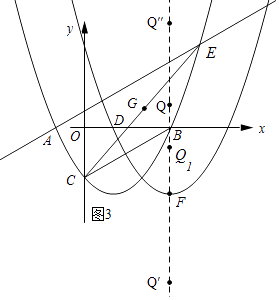
∵y′经过点D,y′的顶点为点F,
∴点F(3,﹣ ![]() ).
).
∵点G为CE的中点,
∴G(2, ![]() ).
).
∴FG= ![]() =
= ![]() .
.
∴当FG=FQ时,点Q(3, ![]() ),Q′(3,
),Q′(3, ![]() ).
).
当GF=GQ时,点F与点Q″关于y= ![]() 对称,
对称,
∴点Q″(3,2 ![]() ).
).
当QG=QF时,设点Q1的坐标为(3,a).
由两点间的距离公式可知:a+ ![]() =
= ![]() ,解得:a=﹣
,解得:a=﹣ ![]() .
.
∴点Q1的坐标为(3,﹣ ![]() ).
).
综上所述,点Q的坐标为(3, ![]() )或′(3,
)或′(3, ![]() )或(3,2
)或(3,2 ![]() )或(3,﹣
)或(3,﹣ ![]() ).
).
【解析】(1)抛物线的解析式可变形为y= ![]() (x+1)(x﹣3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入求得k和b的值,从而得到AE的解析式;(2)设直线CE的解析式为y=mx﹣
(x+1)(x﹣3),从而可得到点A和点B的坐标,然后再求得点E的坐标,设直线AE的解析式为y=kx+b,将点A和点E的坐标代入求得k和b的值,从而得到AE的解析式;(2)设直线CE的解析式为y=mx﹣ ![]() ,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE与点F.设点P的坐标为(x,
,将点E的坐标代入求得m的值,从而得到直线CE的解析式,过点P作PF∥y轴,交CE与点F.设点P的坐标为(x, ![]() x2﹣
x2﹣ ![]() x﹣
x﹣ ![]() ),则点F(x,
),则点F(x, ![]() x﹣
x﹣ ![]() ),则FP=
),则FP= ![]() x2+
x2+ ![]() x.由三角形的面积公式得到△EPC的面积=﹣
x.由三角形的面积公式得到△EPC的面积=﹣ ![]() x2+
x2+ ![]() x,利用二次函数的性质可求得x的值,从而得到点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.然后利用轴对称的性质可得到点G和点H的坐标,当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH;(3)由平移后的抛物线经过点D,可得到点F的坐标,利用中点坐标公式可求得点G的坐标,然后分为QG=FG、QG=QF,FQ=FQ三种情况求解即可.
x,利用二次函数的性质可求得x的值,从而得到点P的坐标,作点K关于CD和CP的对称点G、H,连接G、H交CD和CP与N、M.然后利用轴对称的性质可得到点G和点H的坐标,当点O、N、M、H在条直线上时,KM+MN+NK有最小值,最小值=GH;(3)由平移后的抛物线经过点D,可得到点F的坐标,利用中点坐标公式可求得点G的坐标,然后分为QG=FG、QG=QF,FQ=FQ三种情况求解即可.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
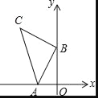
【题目】如图,在平面直角坐标系中,点A的坐标为(﹣2,0),点B的坐标为(0,n),以点B为直角顶点,点C在第二象限内,作等腰直角△ABC.则点C的坐标是_____(用字母n表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是射线CB上的一动点(不与点B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图1,当点D在线段CB上,且∠BAC=90°时,那么∠DCE= 度;
(2)设∠BAC= ![]() ,∠DCE=
,∠DCE= ![]() .
.
① 如图2,当点D在线段CB上,∠BAC≠90°时,请你探究![]() 与
与![]() 之间的数量关系,并证明你的结论;
之间的数量关系,并证明你的结论;
② 如图3,当点D在线段CB的延长线上,∠BAC≠90°时,请将图3补充完整,并直接写出此时![]() 与
与![]() 之间的数量关系(不需证明).
之间的数量关系(不需证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,∠ABC=45°,高线AD、BE相交于点F.
(1)判断BF与AC的数量关系并说明理由;
(2)如图2,将△ACD沿线段AD对折,点C落在BD上的点M,AM与BE相交于点N,当DE∥AM时,判断NE与AC的数量关系并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
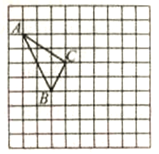
【题目】如图,在正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为A(-4,5),C(-1,3).
(1)请在网格平面内作出平面直角坐标系(不写作法);
(2)请作出△ABC关于y轴对称△A'B'C';
(3)分别写出A'、B'、C'的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y= ![]() x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为(
x2+1具有如下性质:该抛物线上任意一点到定点F(0,2)的距离与到x轴的距离始终相等,如图,点M的坐标为( ![]() ,3),P是抛物线y=
,3),P是抛物线y= ![]() x2+1上一个动点,则△PMF周长的最小值是( )
x2+1上一个动点,则△PMF周长的最小值是( ) 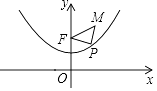
A.3
B.4
C.5
D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
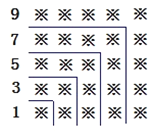
【题目】“数形结合"是一种重要的数学思想,观察下面的图形和算式.
![]()
![]()
![]()
![]()
解答下列问题:
(1)试猜想1+3+5+7+9+…+19=______=( );
(2)试猜想,当n是正整数时,1+3+5+7+9+…+(2n-1)= ;
(3)请用(2)中得到的规律计算:19+21+23+25+27+…+99.
查看答案和解析>>
科目:初中数学 来源: 题型:
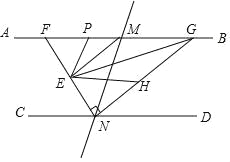
【题目】如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
(1)求证:EM∥NG;
(2)连接EG,在GN上取一点H,使∠HEG=∠HGE,作∠FEH的平分线EP交AB于点P,求∠PEG的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com