
【题目】关于x的一元二次方程x2+(2m+1)x+m2﹣1=0有两个不相等的实数根,求m的取值范围;写出一个满足条件的m的值,并求此方程的根.
科目:初中数学 来源: 题型:
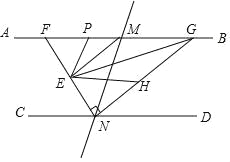
【题目】如图,直线AB∥CD,直线MN与AB,CD分别交于点M,N,ME,NE分别是∠AMN与∠CNM的平分线,NE交AB于点F,过点N作NG⊥EN交AB于点G.
(1)求证:EM∥NG;
(2)连接EG,在GN上取一点H,使∠HEG=∠HGE,作∠FEH的平分线EP交AB于点P,求∠PEG的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如下表和图①:
A | B | C | |
笔试 | 85 | 95 | 90 |
口试 | 80 | 85 |
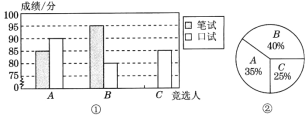
(1)请将表格和图①中的空缺部分补充完整;
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图②(没有弃权票,每名学生只能推荐一人),请计算每人的得票数;
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4∶3∶3的比确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,海边的一段堤岸高出海平面12米,附近的某建筑物高出海平面50米,演习中的某潜水艇在海平面下30米处.
(1)现以海平面的高度为基准,将其记为0米,高于海平面记为正,低于海平面记为负,那么堤岸、附近建筑物及潜水艇的高度各应如何表示?
(2)若以堤岸高度为基准,则堤岸、建筑物及潜水艇的高度又应如何表示?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-2)+(-3)+5
(2)![]() ×5÷
×5÷![]() ×5
×5
(3)12-7×(-4)+8÷(-2)
(4)-14+(2-5)2-2
(5)2÷(-2)+0÷7-(-8)×(-2)
(6)(-1)5×(-5)÷[(-3)2+2×(-5)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式:①a0=1;②a2a3=a5;③2﹣2=﹣ ![]() ;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
;④﹣(3﹣5)+(﹣2)4÷8×(﹣1)=0;⑤x2+x2=2x2 , 其中正确的是( )
A.①②③
B.①③⑤
C.②③④
D.②④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(a),有一张矩形纸片ABCD,其中AD=6cm,以AD为直径的半圆,正好与对边BC相切,将矩形纸片ABCD沿DE折叠,使点A落在BC上,如图(b).则半圆还露在外面的部分(阴影部分)的面积为 . 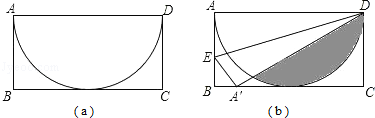
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 . 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com