
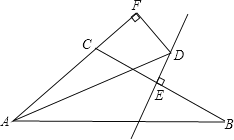
【题目】已知:如图,△ABC中,∠A的平分线AD和边BC的垂直平分线ED相交于点D,过点D作DF垂直于AC交AC的延长线于点F.求证:AB﹣AC=2CF.
【答案】详见解析.
【解析】
根据角平分线的性质首先得出DF=DM,再利用全等三角形的判定定理求出△AFD≌△AMD,即可得出AF=AM,再利用垂直平分线的性质得出CD=BD,进而得出Rt△CDF≌Rt△BDM,即可得出CF=BM,即可得出答案.
证明:连接CD,DB,作DM⊥AB于一点M,
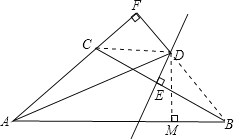
∵AD平分∠A,DF⊥AC,DM⊥AB,
∴DF=DM(角平分线上的点到角的两边距离相等)
∵AD=AD,
∠AFD=∠AMD=90°,
∴△AFD≌△AMD,
∴AF=AM,
∵DE垂直平分线BC,
∴CD=BD(垂直平分线上的点到线段两端点距离相等),
∵FD=DM,∠AFD=∠DMB=90°,
∴Rt△CDF≌Rt△BDM,
∴BM=CF,
∵AB=AM+BM,AF=AC+CF,AF=AM,BM=CF,
∴AB=AC+2CF,
∴AB﹣AC=2CF.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于⊙O,AB为直径,E为AB延长线上的点,作OD∥BC交EC的延长线于点D,连接AD. 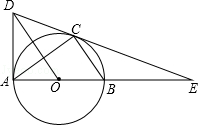
(1)求证:AD=CD;
(2)若DE是⊙O的切线,CD=3,CE=2,求tanE和cos∠ABC的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y= ![]() x与双曲线y=
x与双曲线y= ![]() (x>0)交于点A,将直线y=
(x>0)交于点A,将直线y= ![]() x向下平移个6单位后,与双曲线y=
x向下平移个6单位后,与双曲线y= ![]() (x>0)交于点B,与x轴交于点C,则C点的坐标为;若
(x>0)交于点B,与x轴交于点C,则C点的坐标为;若 ![]() =2,则k= .
=2,则k= . 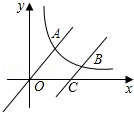
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长阳公园有四棵古树A,B,C,D (单位:米).
(1)请写出A,B,C,D四点的坐标;
(2)为了更好地保护古树,公园决定将如图所示的四边形EFGH用围栏圈起来,划为保护区,请你计算保护区的面积.
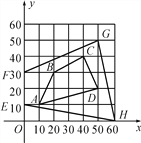
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠1=65°,∠2=65°,∠3=115°.试说明:DE∥BC,DF∥AB.根据图形,完成下面的推理:

因为∠1=65°,∠2=65°,
所以∠1=∠2.
所以______________∥ ( ).
因为AB与DE相交,
所以∠1=∠4( ).
所以∠4=65°.
又因为∠3=115°,
所以∠3+∠4=180°.
所以 ∥ ( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y= ![]() (k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为 .
(k≠0)的图象经过A,B两点,过点A作AC⊥x轴,垂足为C,过点B作BD⊥x轴,垂足为D,连接AO,连接BO交AC于点E,若OC=CD,四边形BDCE的面积为2,则k的值为 . 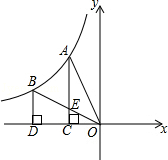
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)(-2)+(-3)+5
(2)![]() ×5÷
×5÷![]() ×5
×5
(3)12-7×(-4)+8÷(-2)
(4)-14+(2-5)2-2
(5)2÷(-2)+0÷7-(-8)×(-2)
(6)(-1)5×(-5)÷[(-3)2+2×(-5)].
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC边上的中线,过点C作AE 的垂线CF,垂足为F,过点B作BD⊥BC,交CF的延长线于点D.
(1)求证:AE=CD.
(2)若AC=12 cm,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,BC=2,点P从点B出发,沿B→C→D向终点D匀速运动,设点P走过的路程为x,△ABP的面积为S,能正确反映S与x之间函数关系的图象是( )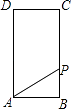
A.
B.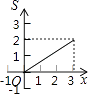
C.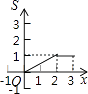
D.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com