练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

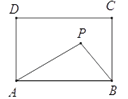
    【题目】如图，在矩形ABCD中，AB＝5，AD＝3，动点P满足，则点P到A、B两点距离之和PA＋PB的最小值为（ ）

    A. B. C. D.

    【答案】D

    【解析】分析：首先由S△PAB=S矩形ABCD，得出动点P在与AB平行且与AB的距离是2的直线l上，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．然后在直角三角形ABE中，由勾股定理求得BE的值，即PA+PB的最小值．

    详解：设△ABP中AB边上的高是h．

    ∵S△PAB=S矩形ABCD，

    ∴ABh=ABAD，

    ∴h=AD=2，

    ∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，连接BE，则BE的长就是所求的最短距离．

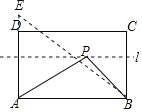
    在Rt△ABE中，∵AB=5，AE=2+2=4，

    ∴BE=，

    即PA+PB的最小值为．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，以点O为端点按顺时针方向依次作射线OA、OB、OC、OD.

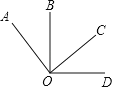
    （1）若∠AOC、∠BOD都是直角，∠BOC＝60°，求∠AOB和∠DOC的度数.

    （2）若∠BOD＝100°，∠AOC＝110°，且∠AOD＝∠BOC+70°，求∠COD的度数.

    （3）若∠AOC＝∠BOD＝α，当α为多少度时，∠AOD和∠BOC互余？并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

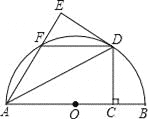
    【题目】如图，AB是半圆O的直径，点C为半径OB上一点，过点C作CD丄AB交半圆O于点D，将△ACD沿AD折叠得到△AED，AE交半圆于点F，连接DF．

    （1）求证：DE是半圆的切线：

    （2）连接0D，当OC=BC时，判断四边形ODFA的形状，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某社区超市第一次用6000元购进甲、乙两种商品，其中乙商品的件数比甲商品件数的倍多15件，甲、乙两种商品的进价和售价如下表：（注：获利＝售价﹣进价）

    甲

    乙

    进价（元/件）

    22

    30

    售价（元/件）

    29

    40

    （1）该超市购进甲、乙两种商品各多少件？

    （2）该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润？

    （3）该超市第二次以第一次的进价又购进甲、乙两种商品，其中甲商品的件数不变，乙商品的件数是第一次的3倍；甲商品按原价销售，乙商品打折销售，第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元，求第二次乙商品是按原价打几折销售？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点O在线段AB上，（不与端点A、B重合），以点O为圆心，OA的长为半径画弧，线段BP与这条弧相切与点P，直线CD垂直平分PB，交PB于点C，交AB于点D，在射线DC上截取DE，使DE＝DB。已知AB＝6，设OA＝r。

    （1）求证：OP∥ED；

    （2）当∠ABP＝30°时，求扇形AOP的面积，并证明四边形PDBE是菱形；

    （3）过点O作OF⊥DE于点F，如图所示，线段EF的长度是否随r的变化而变化？若不变，直接写出EF的值；若变化，直接写出EF与r的关系。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为弘扬中华传统文化，某校举办了学生“国学经典大赛”．比赛项目为：．唐诗；．宋词；．论语；．三字经．比赛形式分“单人组”和“双人组”．

    （1）小丽参加“单人组”，她从中随机抽取一个比赛项目，恰好抽中“三字经”的概率是多少？

    （2）小红和小明组成一个小组参加“双人组”比赛，比赛规则是：同一小组的两名队员的比赛项目不能相同，且每人只能随机抽取一次，则小红和小明都没有抽到“论语”的概率是多少？请用画树状图或列表的方法进行说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲、乙两车从A地出发沿同一路线驶向B地，甲车先出发匀速驶向B地．40分钟后，乙车出发，匀速行驶一段时间后，在途中的货站装货耗时半小时，由于满载货物，为了行驶安全，速度减少了50千米/时，结果与甲车同时到达B地．甲乙两车距A地的路 程y（千米）与乙车行驶时间x（小时）之间的函数图象如图所示．请结合图象信息解答下列问题：

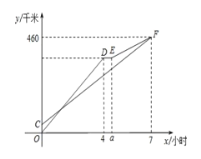
    （1）直接写出a的值，并求甲车的速度；

    （2）求图中线段EF所表示的y与x的函数关系式，并直接写出自变量x的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系 xOy 中，点 A 是一次函数 y 3x 20 与 y x 12的交点，过点 A 分别作 x 、 y 轴的垂线段，垂足分别是 B 和C ，动点 P 和Q 以1个单位/秒的速度，分别从点C 、 B 出发，沿线段CA 、 BO 方向，向终点 A 、O 运动，设运动时间为t秒.

    （1）证明：无论运动时间t 0 t 8取何值，四边形OPAQ 始终为平行四边形；

    （2）当四边形OPAQ 为菱形时，请求出此时 PQ 的长度及直线 PQ 的函数解析式；

    （3）当OP 满足 2 OP 5时，连接 PQ ，直线 PQ 与 y 轴交于点 M ，取线段 AC 的中点 N ，试确定 MNP 的面积 S 与运动的时间t 之间的函数关系式，并求出 S 的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图四个几何体分别是三棱柱，四棱柱，五棱柱和六棱柱，三棱柱有5个面，9条棱，6个顶点，观察图形，填写下面的空．

    （1）四棱柱有　 　个面，　 　条棱，　 　个顶点；

    （2）六棱柱有　 　个面，　 　条棱，　 　个顶点；

    （3）由此猜想n棱柱有　 　个面，　 　条棱，　 　个顶点．

    查看答案和解析>>

    同步练习册答案