
【题目】如图,点O在线段AB上,(不与端点A、B重合),以点O为圆心,OA的长为半径画弧,线段BP与这条弧相切与点P,直线CD垂直平分PB,交PB于点C,交AB于点D,在射线DC上截取DE,使DE=DB。已知AB=6,设OA=r。
(1)求证:OP∥ED;
(2)当∠ABP=30°时,求扇形AOP的面积,并证明四边形PDBE是菱形;
(3)过点O作OF⊥DE于点F,如图所示,线段EF的长度是否随r的变化而变化?若不变,直接写出EF的值;若变化,直接写出EF与r的关系。


【答案】(1)见解析;(2)![]() ,见解析;(3)EF=3
,见解析;(3)EF=3
【解析】试题分析:![]() 根据BP为
根据BP为![]() 的切线,得到
的切线,得到![]() ,
,![]() ,可以推出
,可以推出
![]() ,进而证明平行.
,进而证明平行.
![]() 根据
根据![]() 所对的直角边等于斜边的一半,列出方程,求出半径,根据扇形的面积公式进行即可即可.根据对角线互相垂直平分的四边形是菱形证明.
所对的直角边等于斜边的一半,列出方程,求出半径,根据扇形的面积公式进行即可即可.根据对角线互相垂直平分的四边形是菱形证明.
![]() 根据题意可知,OP∥ED;点
根据题意可知,OP∥ED;点![]() 是
是![]() 的中点,则点
的中点,则点![]() 是
是![]() 的中点,可以用
的中点,可以用![]() 表示出,
表示出,![]() 即可求出
即可求出![]() 的长.
的长.
试题解析:
(1)∵BP为![]() 的切线
的切线
![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴OP∥ED;
(2)在Rt△OBP中,![]()
∴![]()
![]()
在Rt△OBP中,![]()
即![]()
解得:![]()
S扇形AOP=![]() ,
,
证明:∵![]()
∴![]()
∵![]()
∴![]() 是等边三角形
是等边三角形![]()
又∵![]()
∴![]()
∴DE与PB互相垂直平分,
∴四边形PDBE是菱形.
(3)线段EF的长度是不会随r的变化而变化,![]()
根据题意可知,OP∥ED;点![]() 是
是![]() 的中点,则点
的中点,则点![]() 是
是![]() 的中点,
的中点,
![]()
![]()
![]()
![]()
![]()
![]()
线段EF的长度是不会随r的变化而变化,![]()


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
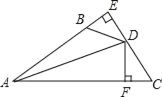
【题目】如图,DE⊥AB于E,DF⊥AC于F,若BD=CD,BE=CF,则下列结论:①DE=DF;②AD平分∠BAC;③AE=AD;④AC﹣AB=2BE中正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在如图所示的方格纸中,点P是∠AOC的边OA上一点,仅用无刻度的直尺完成如下操作:
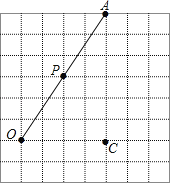
(1)过点P画OC的垂线,垂足为点H;
(2)过点P画OA的垂线,交射线OC于点B;
(3)分别比较线段PB与OB的大小:PB OB(填“>”“<”或“=”),理由是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x+5与x轴交于点A,直线y=﹣x+b与x轴交于点B(1,0),且这两条直线交于点C.
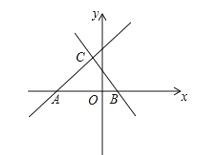
(1)求直线BC的解析式和点C的坐标;
(2)直接写出关于x的不等式x+5>﹣x+b的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
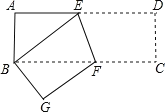
【题目】如图,将长方形 ABCD 沿 EF 折叠,使点 D 与点 B 重合,已知 AB 3 ,AD 9 .
(1)求 BE 的长;
(2)求 EF 的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com