
【题目】如图,在平面直角坐标系 xOy 中,点 A 是一次函数 y 3x 20 与 y x 12的交点,过点 A 分别作 x 、 y 轴的垂线段,垂足分别是 B 和C ,动点 P 和Q 以1个单位/秒的速度,分别从点C 、 B 出发,沿线段CA 、 BO 方向,向终点 A 、O 运动,设运动时间为t秒.

(1)证明:无论运动时间t 0 t 8取何值,四边形OPAQ 始终为平行四边形;
(2)当四边形OPAQ 为菱形时,请求出此时 PQ 的长度及直线 PQ 的函数解析式;
(3)当OP 满足 2![]() OP 5时,连接 PQ ,直线 PQ 与 y 轴交于点 M ,取线段 AC 的中点 N ,试确定 MNP 的面积 S 与运动的时间t 之间的函数关系式,并求出 S 的取值范围.
OP 5时,连接 PQ ,直线 PQ 与 y 轴交于点 M ,取线段 AC 的中点 N ,试确定 MNP 的面积 S 与运动的时间t 之间的函数关系式,并求出 S 的取值范围.
【答案】(1)证明见解析;(2)![]() ,y=-2x+10;(3)S=t(2≤t≤3),2≤S≤3.
,y=-2x+10;(3)S=t(2≤t≤3),2≤S≤3.
【解析】
(1)根据一组对边平行且相等的四边形是平行四边形判断即可;
(2)过P作PH⊥x轴于H,则CP=OH,PH=CO.解方程组求出A的坐标,由菱形的性质以及勾股定理求得t的值,进而得到OQ、OH,HQ的长.利用勾股定理即可求出PQ的长,利用待定系数法可得到直线PQ的解析式.
(3)分别计算出当OP=![]() 和OP=5时,对应的t的值,即可得出t的取值范围.
和OP=5时,对应的t的值,即可得出t的取值范围.
再利用相似三角形的判定与性质表示出MC,然后利用三角形面积公式即可得出结论.
(1)∵0 t 8,∴CP=QB=t.
∵CA=OB,∴PA=OQ.
∵PA∥OQ,∴四边形OPAQ为平行四边形.
(2)过P作PH⊥x轴于H,则CP=OH,PH=CO.
解方程组![]() 得:
得:![]() ,∴A(8,4),∴CO=BA=4,OB=CA=8.
,∴A(8,4),∴CO=BA=4,OB=CA=8.
∵四边形OPAQ 为菱形,∴OP=PA=OQ=8-t.在Rt△CPO中,∵OC2+CP2=OP2,∴![]() ,解得:t=3,∴OQ=8-t=5,OH=CP=3,∴HQ=OQ-OH=5-3=2.
,解得:t=3,∴OQ=8-t=5,OH=CP=3,∴HQ=OQ-OH=5-3=2.
∵PH=CO=4,∴PQ=![]() =
=![]() =
=![]() .
.
∵CP=3,OQ=5,∴P(3,4),Q(5,0).设直线PQ的解析式为y=kx+b,∴![]() ,解得:
,解得:![]() ,∴.设直线PQ的解析式为y=-2x+10.
,∴.设直线PQ的解析式为y=-2x+10.
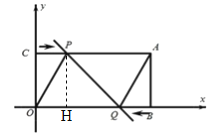
(3)当OP=![]() 时,CP=
时,CP=![]() =2,∴t=2;
=2,∴t=2;
当OP=5时,CP=![]() =3,∴t=3;∴2≤t≤3.
=3,∴t=3;∴2≤t≤3.
∵CP∥OQ,∴△MCP∽△MOQ,∴![]() ,∴
,∴![]() ,解得:MC=
,解得:MC=![]() .
.
∵CA=8,∴CN=4,∴PN=4-t,∴△MNP的面积S=![]() PNCM=
PNCM=![]() =t,∴S=t(2≤t≤3),∴2≤S≤3.
=t,∴S=t(2≤t≤3),∴2≤S≤3.


科目:初中数学 来源: 题型:
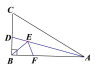
【题目】如图,在Rt△ABC中,AB=6, ∠BAC=30, ∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,则BE+EF的最小值是___
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,延长BC至E点,使CE=![]() BC,点P是AD边上的动点,以
BC,点P是AD边上的动点,以![]() cm/s的速度从D点到A点方向运动,连接AC、CP、DE.
cm/s的速度从D点到A点方向运动,连接AC、CP、DE.
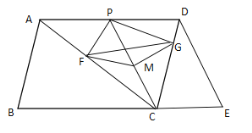
(1)若AD=![]() ,运动时间为t,当四边形PCED为平行四边形时,求t的值;
,运动时间为t,当四边形PCED为平行四边形时,求t的值;
(2)M是CP的中点,PF⊥AC,垂足为F,PG⊥CD,垂足为G,连接MF,MG,求证:∠GMF=2∠ACD.
(3)在(2)的条件下,若∠B=75°,∠ACB=45°,AC=![]() ,连接GF,求△MGF周长的最小值.
,连接GF,求△MGF周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
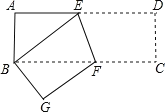
【题目】如图,将长方形 ABCD 沿 EF 折叠,使点 D 与点 B 重合,已知 AB 3 ,AD 9 .
(1)求 BE 的长;
(2)求 EF 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,![]() 为坐标原点,
为坐标原点,![]() 的边
的边![]() 垂直于
垂直于![]() 轴,垂足为
轴,垂足为![]() ,已知
,已知![]() .反比例函数
.反比例函数![]() 的图象经过
的图象经过![]() 的中点
的中点![]() ,交
,交![]() 于点
于点![]() .
.
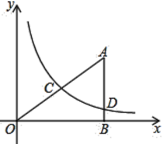
(1)求反比例函数![]() 的表达式;
的表达式;
(2)求经过![]() 、
、![]() 两点的直线所对应的函数表达式;
两点的直线所对应的函数表达式;
(3)设点![]() 是
是![]() 轴上的动点,请直接写出使
轴上的动点,请直接写出使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】瑞瑞有一个小正方体,6个面上分别画有平行四边形、圆、等腰梯形、菱形、等边三角形和直角梯形这6个图形.抛掷这个正方体一次,向上一面的图形既是轴对称图形,又是中心对称图形的概率是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠BAC=90°,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得△AFB,连接EF,下列结论:①△AED≌△AEF;②△ABC的面积等于四边形AFBD的面积;③BE+DC=DE;④BE2+DC2=DE2;⑤∠ADC=22.5°,其中正确的是( )

A. ①③④ B. ③④⑤ C. ①②④ D. ①②⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com