
【题目】如图,在3×3的正方形网格中标出了∠1和∠2.则∠1+∠2= .
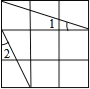
【答案】45°.
【解析】试题分析:根据图形,先将角进行转化,再根据勾股定理的逆定理,求得∠ACB=90°,由等腰三角形的性质,推得∠1+∠2=45°.
解:连接AC,BC.
根据勾股定理,AC=BC=![]() ,AB=
,AB=![]() .
.
∵(![]() )2+(
)2+(![]() )2=(
)2=(![]() )2,
)2,
∴∠ACB=90°,∠CAB=45°.
∵AD∥CF,AD=CF,
∴四边形ADFC是平行四边形,
∴AC∥DF,
∴∠2=∠DAC(两直线平行,同位角相等),
在Rt△ABD中,
∠1+∠DAB=90°(直角三角形中的两个锐角互余);
又∵∠DAB=∠DAC+∠CAB,
∴∠1+∠CAB+∠DAC=90°,
∴∠1+∠DAC=45°,
∴∠1+∠2=∠1+∠DAC=45°.
故答案为:45°.


科目:初中数学 来源: 题型:
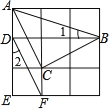
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 边上的一个动点,过点
边上的一个动点,过点![]() 作直线
作直线![]() ,设
,设![]() 交
交![]() 的角平分线于点
的角平分线于点![]() ,交
,交![]() 的外角平分线于点
的外角平分线于点![]() .
.
(1)求证:![]() ;
;
(2)当点![]() 运动到何处时,四边形
运动到何处时,四边形![]() 是矩形?并证明你的结论.
是矩形?并证明你的结论.
(3)当点![]() 运动到何处,且
运动到何处,且![]() 满足什么条件时,四边形
满足什么条件时,四边形![]() 是正方形?并说明理由.
是正方形?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
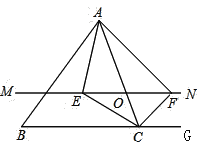
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程).有下列说法:

①“龟兔再次赛跑”的路程为1000米;
②兔子和乌龟同时从起点出发;
③乌龟在途中休息了10分钟;
④兔子在途中750米处追上乌龟.
其中正确的说法是 .(把你认为正确说法的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,C为线段AB上一点,点D为BC的中点,且AB=18cm,AC=4CD.
(1)图中共有 条线段;
(2)求AC的长;
(3)若点E在直线AB上,且EA=2cm,求BE的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
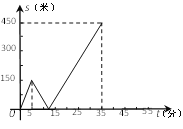
【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距![]() (米),甲行走的时间为
(米),甲行走的时间为![]() (分),
(分),![]() 关于
关于![]() 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.
(1)求甲行走的速度;
(2)在坐标系中,补画![]() 关于
关于![]() 函数图象的其余部分;
函数图象的其余部分;
(3)问甲、乙两人何时相距360米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:由绝对值的意义可知:当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程
.利用这一特性,可以帮助我们解含有绝对值的方程.比如:方程![]() ,
,
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() ;
;
当![]() 时,原方程可化为
时,原方程可化为![]() ,解得
,解得![]() .
.
所以原方程的解是![]() 或
或![]() .
.
(1)请补全题目中横线上的结论.
(2)仿照上面的例题,解方程:![]() .
.
(3)若方程![]() 有解,则
有解,则![]() 应满足的条件是 .
应满足的条件是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一张三角形纸片ABC中,AB=10cm,BC=7cm,AC=6cm,沿过点B的直线折叠这个三角形,使顶点C落在边AB上的点E处,折痕为BD.

(1)求△AED的周长.
(2)说明BD垂直平分EC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景知识)
数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合.研究数轴我们发现了许多重要的规律:若数轴上点![]() 、点
、点![]() 表示的数分别为
表示的数分别为![]() 、
、![]() ,则
,则![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ,线段
,线段![]() 的中点表示的数为
的中点表示的数为![]() .
.
(问题情境)
如图,数轴上点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为8,点
表示的数为8,点![]() 从点
从点![]() 出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点
出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点![]() 从点
从点![]() 出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为
出发,以每秒2个单位长度的速度向左匀速运动,设运动时间为![]() 秒(
秒(![]() ).
).
(综合运用)
(1)填空:
①![]() 、
、![]() 两点之间的距离
两点之间的距离![]() ________,线段
________,线段![]() 的中点表示的数为__________.
的中点表示的数为__________.
②用含![]() 的代数式表示:
的代数式表示:![]() 秒后,点
秒后,点![]() 表示的数为____________;点
表示的数为____________;点![]() 表示的数为___________.
表示的数为___________.
③当![]() _________时,
_________时,![]() 、
、![]() 两点相遇,相遇点所表示的数为__________.
两点相遇,相遇点所表示的数为__________.
(2)当![]() 为何值时,
为何值时,![]() .
.
(3)若点![]() 为
为![]() 的中点,点
的中点,点![]() 为
为![]() 的中点,点
的中点,点![]() 在运动过程中,线段
在运动过程中,线段![]() 的长度是否发生变化?若变化,请说明理由;若不变,请求出线段
的长度是否发生变化?若变化,请说明理由;若不变,请求出线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=x+5与x轴交于点A,直线y=﹣x+b与x轴交于点B(1,0),且这两条直线交于点C.
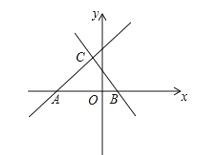
(1)求直线BC的解析式和点C的坐标;
(2)直接写出关于x的不等式x+5>﹣x+b的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com