
【题目】如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M分别作MD⊥AC于点D, 作ME⊥CB于点E.
(1) 求证:四边形DMEC是矩形.
(2) 求线段DE的最小值.

【答案】(1)证明见解析;(2)线段DE的最小值为![]() .
.
【解析】试题分析:(1)由MD⊥AC,ME⊥CB及∠C=90°,根据有三个角是直角的四边形是矩形即可得;
(2)连接CM,由四边形CDME是矩形,可得DE=CM, 由垂线段最短可知当CM⊥AB时,CM最短, 根据面积法求出AB边上的高即可.
试题解析:(1)∵MD⊥AC,ME⊥CB,∴∠MDC=∠MEC=90°,
又∵∠C=90°,∴ 四边形CDME是矩形;
(2)连接CM,如图所示:
∵四边形CDME是矩形,∴DE=CM,
∵∠C=90°,BC=3,AC=4,∴ AB=![]() =
=![]() =5,
=5,
当CM⊥AB时,CM最短, 此时△ABC的面积=![]() ABCM=
ABCM=![]() BCAC,
BCAC,
∴CM的最小值=![]() =
=![]() ,
,
∴线段DE的最小值为![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某商场以每件42元的价格购进一种服装,由试销知,每天的销量t与每件的销售价x(元)之间的函数关系为t=204-3x。
(1)试写出每天销售这种服装的毛利润y(元)与每件销售价x(元)之间的函数表达式(毛利润=销售价-进货价); 并求出自变量的取值范围。
(2)每件销售价为多少元,才能使每天的毛利润最大?最大毛利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是反映世界人口情况的数据:1957年、1974年、1987年、1999年的世界人口数依次为30亿、40亿、50亿、60亿,预计2050年世界人口将达90亿.上面的数据不能制成( )
A. 统计表B. 条形统计图
C. 折线统计图D. 扇形统计图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】算式-7+4-6-10读作____________________________________,也可读作________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两人要去某风景区游玩,每天某—时段开往该风景区有三辆汽车(票价相同),但是他们不知道这些车的舒适程度,也不知道汽车开过来的顺序,两人采用了不同的乘车方案:
甲无论如何总是上开来的第一辆车,而乙则是先观察后上车,当第一辆车开来时,他不上车,而是仔细观察车的舒适状况,如果第二辆乍的状况比第一辆好,他就上第二辆车;如果第二辆不比第—辆好,他就上第三辆车.若把这三辆车的舒适程度分为上、中、下三等.请问:
(1)三辆车按出现的先后顺序共有哪几种不同的可能?
(2)你认为甲、乙两人采用的方案,哪一种方案使自己乘坐上等车的可能性大?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年2班组织了一次经典诵读比赛,甲乙两组各10人的比赛成绩如下表(10分制):

(I)甲组数据的中位数是 ,乙组数据的众数是 ;
(Ⅱ)计算乙组数据的平均数和方差;
(Ⅲ)已知甲组数据的方差是1.4分2,则成绩较为整齐的是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
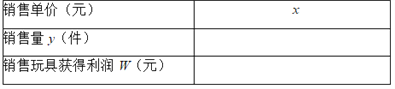
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
(2)在(1)条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com