
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
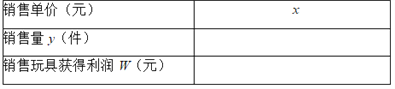
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
(2)在(1)条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
【答案】(1)填表见解析;
(2)玩具销售单价为50元或80元时,可获得10000元销售利润;
(3)商场销售该品牌玩具获得的最大利润为8640元.
【解析】试题分析:(1)由销售单价每涨1元,就会少售出10件玩具得y=600-(x-40)×10=1000-10x,利润=(1000-10x)(x-30)=-10x2+1300x-30000;
(2)令-10x2+1300x-30000=10000,求出x的值即可;
(3)首先求出x的取值范围,然后把w=-10x2+1300x-30000转化成y=-10(x-65)2+12250,结合x的取值范围,求出最大利润.
试题解析:(1)
销售单价(元) | x |
销售量y(件) | 1000-10x |
销售玩具获得利润w(元) | -10x2+1300x-30000 |
(2)-10x2+1300x-30000=10000
解之得:x1=50,x2=80
答:玩具销售单价为50元或80元时,可获得10000元销售利润,
(3)根据题意得
![]()
解之得:44≤x≤46,
w=-10x2+1300x-30000=-10(x-65)2+12250,
∵a=-10<0,对称轴是直线x=65,
∴当44≤x≤46时,w随x增大而增大.
∴当x=46时,W最大值=8640(元).
答:商场销售该品牌玩具获得的最大利润为8640元.
考点: 1.二次函数的应用;2.一元二次方程的应用.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M分别作MD⊥AC于点D, 作ME⊥CB于点E.
(1) 求证:四边形DMEC是矩形.
(2) 求线段DE的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a<0)的对称轴为x=1,交x轴的一个交点为(x1,0),且﹣1<x1<0,有下列5个结论:①abc>0;②9a﹣3b+c<0;③2c<3b;④(a+c)2<b2;⑤a+b>m(am+b)(m≠1的实数)其中正确的结论有( )
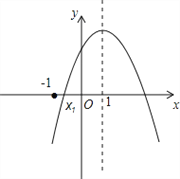
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴相交于两点A(1,0),B(3,0),与y轴相交于点C(0,3).
(1)求抛物线的函数关系式.
(2)将y=ax2+bx+c化成y=a(x﹣m)2+k的形式(请直接写出答案).
(3)若点D(3.5,m)是抛物线y=ax2+bx+c上的一点,请求出m的值,并求出此时△ABD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场出售一批进价为2元的贺卡,在市场营销中发现商品的日销售单价x元与日销售量y个之间有如下关系:
x(元/个) | 3 | 4 | 5 | 6 |
y(个) | 20 | 15 | 12 | 10 |
(1)根据表中数据,在直角坐标系描出实数对(x,y)的对应点
(2)猜测并确定y与x之间的函数关系式,并画出图象;
(3)设经营此贺卡的销售利润为W元,试求出W与x之间的函数关系式,若物价局规定此贺卡的售价最高不能超过10元/个,请你求出当日销售单价x定为多少元时,才能获得最大日销售利润?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com