
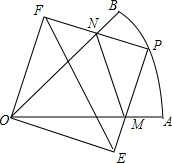
 如图,在半径为1的扇形AOB中∠AOB=45°,P为弧AB上一动点(不与A,B重合),以OP为对角线作正方形OEPF,分别交OA,OB于M,N,给出以下结论:
如图,在半径为1的扇形AOB中∠AOB=45°,P为弧AB上一动点(不与A,B重合),以OP为对角线作正方形OEPF,分别交OA,OB于M,N,给出以下结论:分析 连接OP,由$\widehat{BP}=\widehat{AP}$得出∠BOP=∠AOP,由正方形的性质得出OF=PF=PE=OE,∠EOF=∠OFN=∠OEM=90°,∠POF=∠POE=45°,得出∠FON=∠EOM,由ASA即可证明△OFN≌△OEM,得出①正确;
由△OFN≌△OEM,得出FN=EM,得出PN=PM,因此PN:FN=PM:EM,即可证出MN∥EF;得出②正确;
延长ME至D,使ED=NF,连接OD;先证明△OED≌△OFN,得出OD=ON,∠EOD=∠FON,证出∠MOD=∠MON,由SAS证明△MOD≌△MON,得出MD=MN,即可得出EM+NF=MN,得出③正确;
由于点P在弧AB上运动,因此∠PNM不一定等于45°,得出④不正确.
解答 解:①正确;理由如下:连接OP,如图1所示: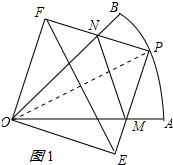
∵点P为弧AB中点,
∴$\widehat{BP}=\widehat{AP}$,
∴∠BOP=∠AOP=$\frac{1}{2}$∠AOB=22.5°,
∵四边形OEPF是正方形,
∴OF=PF=PE=OE,∠EOF=∠OFN=∠OEM=90°,∠POF=∠POE=45°,
∴∠FON=∠EOM,
在△OFN和△OEM中,
$\left\{\begin{array}{l}{∠OFN=∠OEM}&{\;}\\{OF=OE}&{\;}\\{∠FON=∠EOM}&{\;}\end{array}\right.$,
∴△OFN≌△OEM(ASA);
②正确;理由如下:
∵△OFN≌△OEM,
∴FN=EM,
∴PN=PM,
∴PN:FN=PM:EM,
∴MN∥EF;
③正确;延长ME至D,使ED=NF,连接OD;如图2所示: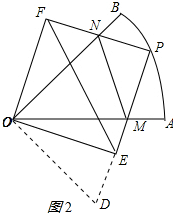 则∠OED=90°,
则∠OED=90°,
在△OED和△OFN中,
$\left\{\begin{array}{l}{OE=OF}&{\;}\\{∠OED=∠OFN=90°}&{\;}\\{ED=FN}&{\;}\end{array}\right.$,
∴△OED≌△OFN(SAS),
∴OD=ON,∠EOD=∠FON,
∴∠NOD=90°,
∵∠AOB=45°,
∴∠MOD=45°,
∴∠MOD=∠MON,
在△MOD和△MON中,
$\left\{\begin{array}{l}{OD=ON}&{\;}\\{∠MOD=∠MON}&{\;}\\{OM=OM}&{\;}\end{array}\right.$,
∴△MOD≌△MON(SAS),
∴MD=MN,
即EM+ED=MN,
∴EM+NF=MN;
④不正确;∵点P在弧AB上运动,
∴∠PNM不一定等于45°;
正确结论的序号是①②③.
故答案为:①②③.
点评 本题是圆的综合题目,考查了圆周角定理、正方形的性质、全等三角形的判定与性质、平行线的判定等知识;本题难度较大,综合性强,特别是③中,需要通过作辅助线证明两次三角形全等才能得出结论.


科目:初中数学 来源: 题型:选择题
| A. | 图象必经过点(-1,3) | B. | 若x>1,则-3<y<0 | ||
| C. | 图象在第二、四象限内 | D. | y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com