Question

如图，D是等边△ABC的AC边上的中点，点E在BC的延长线上，DE=DB，△ABC的周长是9，则∠E=__________°，CE=__________．

Answer 1

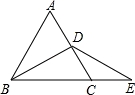
30°，CE=1.5．

【考点】等边三角形的性质；等腰三角形的性质．

【分析】由△ABC为等边三角形，且BD为边AC的中线，根据“三线合一”得到BD平分∠ABC，而∠ABC为60°，得到∠DBE为30°，又因为DE=DB，根据等边对等角得到∠E与∠DBE相等，故∠E也为30°；

由等边三角形的三边相等且周长为9，求出AC的长为3，且∠ACB为60°，根据∠ACB为△DCE的外角，根据三角形的外角等于与它不相邻的两个内角之和，求出∠CDE也为30°，根据等角对等边得到CD=CE，都等于边长AC的一半，从而求出CE的值．

【解答】解：∵△ABC为等边三角形，D为AC边上的中点，

∴BD为∠ABC的平分线，且∠ABC=60°，

即∠DBE=30°，又DE=DB，

∴∠E=∠DBE=30°，

∵等边△ABC的周长为9，

∴AC=3，且∠ACB=60°，

∴∠CDE=∠ACB﹣∠E=30°，即∠CDE=∠E，

∴CD=CE=AC=．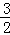

故答案为：30；．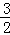

【点评】此题考查了等边三角形的性质，利用等边三角形的性质可以解决角与边的有关问题，尤其注意等腰三角形“三线合一”性质的运用，及“等角对等边”、“等边对等角”的运用．