
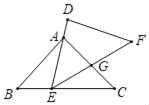
【题目】如图,在△ABC中,已知,AB=AC=6,BC=10.E是C边上一动点(E不与点B、C重合),△DEF≌△ABC.其中点A,B的对应点分别是点D、E,且点E在运动时,DE边始终经过点A,设EF与AC相交于点G,当△AEG为等腰三角形时,则BE的长为_____.
【答案】4或6.4.
【解析】
题目要求△AEG为等腰三角形,但没有说明哪两边为腰,这种一般都要分情况讨论,根据![]() ,且
,且![]() 为
为![]() 的外角,可得
的外角,可得![]() ,所以
,所以![]() ,首先排除一种情况,剩下两种
,首先排除一种情况,剩下两种![]() 与
与![]() ,根据全等三角形与相似三角形的性质求解即可.
,根据全等三角形与相似三角形的性质求解即可.
解:∵∠AEF=∠B=∠C,且∠AGE>∠C,
∴∠AGE>∠AEF,
∴AE≠AG;
当AE=EG时,则△ABE≌△ECG,
∴CE=AB=6,
∴BE=BC﹣EC=10﹣6=4;
当AG=EG时,则∠GAE=∠GEA,
∴∠GAE+∠BAE=∠GEA+∠CEG,
即∠CAB=∠CEA,
又∵∠C=∠C,
∴△CAE∽△CBA,
∴![]() =
=![]() ,
,
∴CE=![]() =
=![]() =3.6,
=3.6,
∴BE=10﹣3.6=6.4;
∴BE=4或6.4.
故答案为4或6.4.



 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
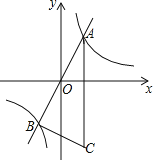
【题目】如图,反比例函数y=![]() (k≠0)的图象与正比例函数y=2x的图象相交于A(1,a)、B两点,点C在第四象限,CA∥y轴,且CB⊥AB.
(k≠0)的图象与正比例函数y=2x的图象相交于A(1,a)、B两点,点C在第四象限,CA∥y轴,且CB⊥AB.
(1)求反比例函数的解析式及点B的坐标;
(2)求tanC的值和△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”,后人称其为“赵爽弦图”.如图是由弦图变化得到的,它由八个全等的直角三角形拼接而成,记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为S1、S2、S3.若S1+S2+S3=10,则S2的值为( )
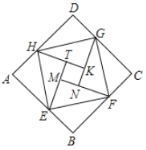
A.![]() B.
B.![]() C.3D.
C.3D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场同时购进甲、乙两种商品共100件,其进价和售价如下表:
商品名称 | 甲 | 乙 |
进价(元/件) | 40 | 90 |
售价(元/件) | 60 | 120 |
设其中甲种商品购进x件,商场售完这100件商品的总利润为y元.
(Ⅰ)写出y关于x的函数关系式;
(Ⅱ)该商场计划最多投入8000元用于购买这两种商品,
①至少要购进多少件甲商品?
②若销售完这些商品,则商场可获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,G是BC的中点,过A、D、G三点的圆O与边AB、CD分别交于点E、点F,给出下列说法,其中正确说法的个数是( )
(1)AC与BD的交点是圆O的圆心;
(2)AF与DE的交点是圆O的圆心;
(3)![]() ;
;
(4)DE>DG,
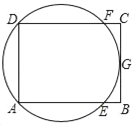
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于长度为4的线段AB(图1),小若用尺规进行如下操作(图2)根据作图痕迹,有下列说法:①△ABC是等腰三角形;②△ABC是直角三角形;③△ABC是等边三角形;④弧AD的长度为![]() ,⑤△ABC是直角三角形的依据是直径所对的圆周角为直角,则其中正确的个数是( )
,⑤△ABC是直角三角形的依据是直径所对的圆周角为直角,则其中正确的个数是( )
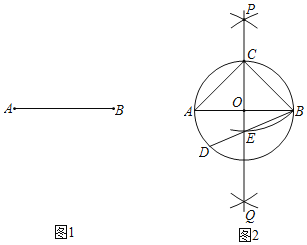
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】人们利用“公众号”进行学习和获取信息已成为了生活常态,为了解某个学习类公众号的推广情况,小方同学调查统计了从周一到周五对该公众号进行关注的“粉丝”人数的变化情况,并将结果绘制成如图1和图2所示的两个不完整的统计图

根据以上信息,完成下面的问题:
(1)如图2,周三进行关注的“粉丝”人数对应的扇形圆心角是 °;
(2)将折线统计图补充完整;
(3)在原来基础上,小方对该公众号又统计了后续周六和周日关注的“粉丝”人数发现这7天平均每天关注的“粉丝”人数比前5天平均每天关注的“粉丝”人数多2人,则
①周六和周日这两天关注了该公众号的一共是 人;
②现从周六关注公众号的前3位男士“粉丝”和周日关注公众号的前2位女士“粉丝”中,随机抽取两位进行奖励,请用列表法或者画树状图的方法,求所抽取的两位“粉丝”恰好是一男一女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PHPC
其中正确的是( )

A. ①②③④ B. ②③ C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一名大学生利用“互联网+”自主创业,销售一种产品,这种产品的成本价为24元/件,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于32元件,市场调查发现,该产品每天的销售最![]() (件)与
(件)与![]() (元/件)之间的函数关系如图所示.
(元/件)之间的函数关系如图所示.
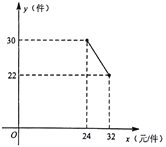
(1)求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)求每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元/件)之问的函数关系式并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
(元/件)之问的函数关系式并求出每天销售价为多少元时,每天的销售利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com