
科目:初中数学 来源: 题型:解答题
| 等待时间x | 1 | 2 | 5 | 10 | 20 |
| 舒适度指数y | 100 | 50 | 20 | 10 | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
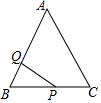 如图,等边△ABC的边长为6,P沿C→B→A运动,Q沿B→A→C运动,且速度都为每秒2个单位,△BPQ面积为y,则y与运动时间x秒的函数的图象大致为( )
如图,等边△ABC的边长为6,P沿C→B→A运动,Q沿B→A→C运动,且速度都为每秒2个单位,△BPQ面积为y,则y与运动时间x秒的函数的图象大致为( )| A. | 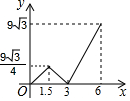 | B. | 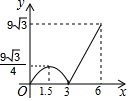 | C. | 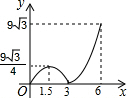 | D. | 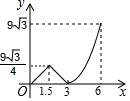 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
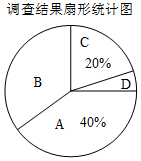 某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:
某课外活动小组为了解本校学生上学常用的一种交通方式,随机调查了本校部分学生,根据调查结果,统计整理并制作了如图尚不完整的统计图表:| 组别 | 上学常用的一种交通方式 | 频数(人数) |
| A | 步行 | 64 |
| B | 骑自行车 | m |
| C | 乘公交车 | n |
| D | 其它 | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
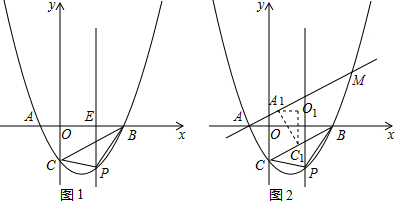
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
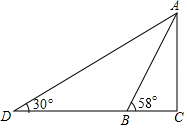 如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)
如图,某游乐园有一个滑梯高度AB,高度AC为3米,倾斜角度为58°.为了改善滑梯AB的安全性能,把倾斜角由58°减至30°,调整后的滑梯AD比原滑梯AB增加多少米?(精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 平均数是80 | B. | 极差是15 | C. | 中位数是80 | D. | 众数是75 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com