

分析 (1)由△AOB≌△AOC,推出∠C=∠B,由OA=OC,推出∠OAC=∠C=∠B,由∠ADO=∠ADB,即可证明△OAD∽△ABD;
(2)如图2中,当△OCD是直角三角形时,需要分类讨论解决问题;
(3)如图3中,作OH⊥AC于H,设OD=x.想办法用x表示AD、AB、CD,再证明AD2=AC•CD,列出方程即可解决问题;
解答 (1)证明:如图1中,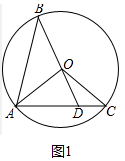
在△AOB和△AOC中,
$\left\{\begin{array}{l}{OA=OA}\\{AB=AC}\\{OB=OC}\end{array}\right.$,
∴△AOB≌△AOC,
∴∠C=∠B,
∵OA=OC,
∴∠OAC=∠C=∠B,
∵∠ADO=∠ADB,
∴△OAD∽△ABD.
(2)如图2中,①当∠ODC=90°时,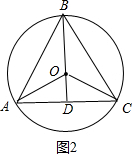
∵BD⊥AC,OA=OC,
∴AD=DC,
∴BA=BC=AC,
∴△ABC是等边三角形,
在Rt△OAD中,∵OA=1,∠OAD=30°,
∴OD=$\frac{1}{2}$OA=$\frac{1}{2}$,
∴AD=$\sqrt{O{A}^{2}-O{D}^{2}}$=$\frac{\sqrt{3}}{2}$,
∴BC=AC=2AD=$\sqrt{3}$.
②∠COD=90°,∠BOC=90°,BC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
③∠OCD显然≠90°,不需要讨论.
综上所述,BC=$\sqrt{3}$或$\sqrt{2}$.
(3)如图3中,作OH⊥AC于H,设OD=x.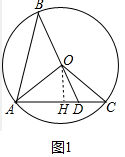
∵△DAO∽△DBA,
∴$\frac{AD}{DB}$=$\frac{OD}{AD}$=$\frac{OA}{AB}$,
∴$\frac{AD}{x+1}$=$\frac{x}{AD}$=$\frac{1}{AB}$,
∴AD=$\sqrt{x(x+1)}$,AB=$\frac{\sqrt{x(x+1)}}{x}$,
∵S2是S1和S3的比例中项,
∴S22=S1•S3,
∵S2=$\frac{1}{2}$AD•OH,S1=S△OAC=$\frac{1}{2}$•AC•OH,S3=$\frac{1}{2}$•CD•OH,
∴($\frac{1}{2}$AD•OH)2=$\frac{1}{2}$•AC•OH•$\frac{1}{2}$•CD•OH,
∴AD2=AC•CD,
∵AC=AB.CD=AC-AD=$\frac{\sqrt{x(x+1)}}{x}$-$\sqrt{x(x+1)}$,
∴($\sqrt{x(x+1)}$)2=$\frac{\sqrt{x(x+1)}}{x}$•($\frac{\sqrt{x(x+1)}}{x}$-$\sqrt{x(x+1)}$),
整理得x2+x-1=0,
解得x=$\frac{\sqrt{5}-1}{2}$或$\frac{-\sqrt{5}-1}{2}$,
经检验:x=$\frac{\sqrt{5}-1}{2}$是分式方程的根,且符合题意,
∴OD=$\frac{\sqrt{5}-1}{2}$.
(也可以利用角平分线的性质定理:$\frac{AD}{AC}$=$\frac{AD}{AB}$=$\frac{DO}{OB}$,黄金分割点的性质解决这个问题)
点评 本题考查圆的综合题、全等三角形的判定和性质、相似三角形的判定和性质、比例中项等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,属于中考压轴题.


科目:初中数学 来源: 题型:选择题
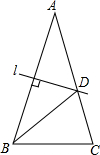 如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )
如图,在△ABC中,AB=AC,∠A=30°,AB的垂直平分线l交AC于点D,则∠CBD的度数为( )| A. | 30° | B. | 45° | C. | 50° | D. | 75° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 8.8分,8.8分 | B. | 9.5分,8.9分 | C. | 8.8分,8.9分 | D. | 9.5分,9.0分 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
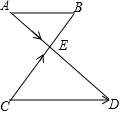 如图,已知AB∥CD,CD=2AB,AD、BC相交于点E,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{CE}$=$\overrightarrow{b}$,那么向量$\overrightarrow{CD}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\overrightarrow{b}$+2$\overrightarrow{a}$.
如图,已知AB∥CD,CD=2AB,AD、BC相交于点E,设$\overrightarrow{AE}$=$\overrightarrow{a}$,$\overrightarrow{CE}$=$\overrightarrow{b}$,那么向量$\overrightarrow{CD}$用向量$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\overrightarrow{b}$+2$\overrightarrow{a}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
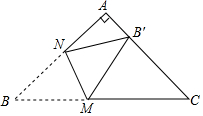 如图,在Rt△ABC中,∠A=90°,AB=AC,BC=$\sqrt{2}$+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$或1.
如图,在Rt△ABC中,∠A=90°,AB=AC,BC=$\sqrt{2}$+1,点M,N分别是边BC,AB上的动点,沿MN所在的直线折叠∠B,使点B的对应点B′始终落在边AC上,若△MB′C为直角三角形,则BM的长为$\frac{1}{2}$$\sqrt{2}$+$\frac{1}{2}$或1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,抛物线y=ax2+bx+2经过点A(-1,0),B(4,0),交y轴于点C;
如图,抛物线y=ax2+bx+2经过点A(-1,0),B(4,0),交y轴于点C;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com