
【题目】在平面直角坐标系xOy中,A(a,0),B(0,b)其中a,b满足![]() .点C为x轴正半轴上的一点,且点C在点A右侧,若点D为第一象限内一点,且满足CD⊥CB,
.点C为x轴正半轴上的一点,且点C在点A右侧,若点D为第一象限内一点,且满足CD⊥CB,![]() .
.
(1)求A,B的坐标;
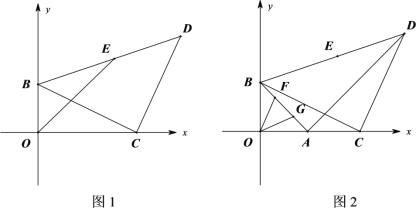
(2)如图1,点E为BD中点,连接OE,求证:![]() ;
;
(3)如图2,若点F、G是BA上的两个动点,且![]() ,求证:
,求证:![]() .
.
【答案】(1)![]() (2)证明见解析 (3)证明见解析
(2)证明见解析 (3)证明见解析
【解析】
(1)根据二次根式和平方的非负性可得![]() ,即可求出A,B的坐标;
,即可求出A,B的坐标;
(2)作![]() 与x轴交于点F,连接CE、EF,通过证明
与x轴交于点F,连接CE、EF,通过证明![]() 和
和![]() ,可得△EFO是等腰直角三角形,即可得证
,可得△EFO是等腰直角三角形,即可得证![]() ;
;
(3)将△BOF绕O点顺时针旋转90°得△AOH,旋转后点B与点A重合,点F对应点H,连接HG,根据旋转的性质得![]() ,再通过证明
,再通过证明![]() ,可得
,可得![]() ,根据勾股定理得
,根据勾股定理得![]() ,即可得证
,即可得证![]() .
.
(1)∵a,b满足![]()
∴![]()
解得![]()
∴![]() ;
;
(2)作![]() 与x轴交于点F,连接CE、EF
与x轴交于点F,连接CE、EF
∵![]() ,
,![]()
∴![]() ,△BCD是等腰直角三角形
,△BCD是等腰直角三角形
∴![]()
∵![]()
∴![]()
∴![]()
在△span>BOC和△CFD中
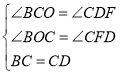
∴![]()
∴![]() ,
,![]()
∵点E为BD中点
∴![]() ,
,![]()
∴![]()
∴![]()
∴![]()
在△BOE和△CFE中
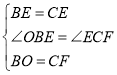
∴![]()
∴![]() ,
,![]()
∵![]()
∴![]()
∴△EFO是等腰直角三角形
∴![]() ;
;
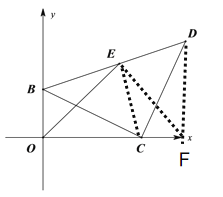
(3)将△BOF绕O点顺时针旋转90°得△AOH,旋转后点B与点A重合,点F对应点H,连接HG
根据旋转的性质得
![]() ,
,![]() ,
,![]() ,
,![]()
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]()
在△FOG和△HOG中
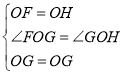
∴![]()
∴![]()
在Rt△GAH中
![]()
∴![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
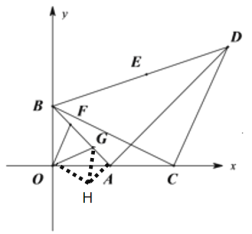
【题目】如图,双曲线y=![]() (x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3),BE⊥x轴,垂足为E.
(1)确定k的值;
(2)若点D(3,m)在双曲线上,求直线AD的解析式;
(3)计算△OAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车专卖店销售A,B两种型号的新能源汽车.上周售出1辆A型车和3辆B型车,销售额为96万元;本周已售2辆A型车和1辆B型车,销售额为62万元.
(1)求每辆A型车和B型车的售价各多少万元.
(2)甲公司拟向该店购买A,B两种型号的新能源汽车共6辆,购车费不少于130万元,且不超过140万元. 则有哪几种购车方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为了检验两枚六个面分别刻有点数1、 2、3、4、5、6的正六面体骰子的质量是否都合格,在相同的条件下,同时抛两枚骰子20 00 0次,结果发现两个朝上面的点数和是7的次数为20次.你认为这两枚骰子质量是否都合格(合格标准为:在相同条件下抛骰子时,骰子各个面朝上的机会相等)?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两位同学做抛骰子(均匀正方体形状)实验,他们共抛了60次,出现向上点数的次数如表:
向上点数 | 1 | 2 | 3 | 4 | 5 | 6 |
出现次数 | 8 | 10 | 7 | 9 | 16 | 10 |
(1)计算出现向上点数为6的频率.
(2)丙说:“如果抛600次,那么出现向上点数为6的次数一定是100次.”请判断丙的说法是否正确并说明理由.
(3)如果甲乙两同学各抛一枚骰子,求出现向上点数之和为3的倍数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)与直线y=-x相交于A,B两点,则下列说法正确的是( )
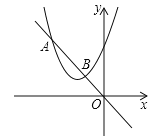
A. ac<0,(b+1)2-4ac<0 B. ac<0,(b+1)2-4ac>0
C. ac>0,(b+1)2-4ac<0 D. ac>0,(b+1)2-4ac>0
查看答案和解析>>
科目:初中数学 来源: 题型:
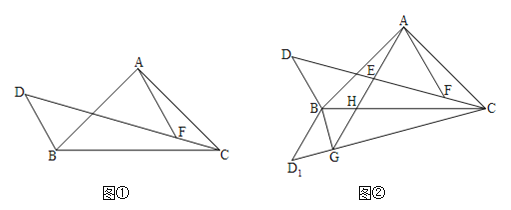
【题目】已知△ABC,AB=AC,∠BAC=90°,D为△ABC外部一点,∠BDC=45°,点F在CD上且AF∥DB.
(1)如图①,求证:![]() ;
;
(2)如图②,将△BCD沿BC翻折得到△BCD1,过点B作BG⊥CD1,垂足为G,连接AG交CD于E,交BC于H.若AF=![]() ,∠BCD=15°,求AG的长度.
,∠BCD=15°,求AG的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com