
����Ŀ���з��̽�Ӧ���⣺
��1��ij����������֯��һ������Ϊ��ϣ��������ļ�裬���۳�1000����Ʊ����֪����Ʊÿ��8Ԫ��ѧ��Ʊÿ��5Ԫ������Ʊ��6950Ԫ������Ʊ��ѧ��Ʊ������
��2��ij������һ����ɫ�߲ˣ������г���ֱ�����ۣ�ÿ������Ϊ1000Ԫ�����ּӹ������ۣ�ÿ������ɴ�4500Ԫ�������ӹ������ۣ�ÿ����������7500Ԫ������һ��ũ���̹�˾�ջ������߲�140�֣��ù�˾�ӹ������������ǣ�������߲˽��дּӹ���ÿ��ɼӹ�16�֣�������о��ӹ���ÿ��ɼӹ�6�֣������ּӹ���ʽ����ͬʱ���У��ܼ��ڵ��������ƣ���˾������15���ڽ������߲�ȫ�����ۻ�ӹ���ϣ�Ϊ�˹�˾���������ֿ��з�����
����һ�����߲�ȫ�����о��ӹ���û���ü����о��ӹ���ֱ�ӳ���
�������������ܶ�ض��߲˽��дּӹ���û�����ü����мӹ����߲ˣ����г���ֱ�����ۣ�
���������������߲˽��о��ӹ��������߲˽��дּӹ�����ǡ��15����ɣ�
����Ϊѡ�����ַ���������ࣿΪʲô��
���𰸡�(1) ����Ʊ650�ţ���ͯƱ350������2��������������࣮
��������
����һ�ͷ������Ļ��������ֱ�����,������: �辫�ӹ�x��, �����е���ȹ�ϵ��: ���ӹ�������+�ּӹ�������=15��.��:![]() , �Ϳ����г�����. ������ӹ��ʹּӹ�������,�Ӷ��������. Ȼ��ȽϿɵó���.
, �Ϳ����г�����. ������ӹ��ʹּӹ�������,�Ӷ��������. Ȼ��ȽϿɵó���.
�⣺��1�������Ʊx�ţ����ͯƱΪ��1000��x���ţ�
������ã�8x+5��1000��x��=6950��
��ã�x=650��
��1000��x=1000��650=350�ţ�
�ʳ���Ʊ650�ţ���ͯƱ350�ţ�
��2������һ������7500��90+1000����140��90��=72. 5��
������������140��4500=63��
������������
�辫�ӹ���x�֣���ּӹ��ˣ�140��x���֣�
![]() ��
��
��ã�x=60��
������x=60��ԭ���̵Ľ⣮
��7500��60+4500����140��60��=81��
���Է�����������࣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD��AB��9��AD��4. EΪCD����һ�㣬CE��6.
��1����AE�ij���
��2����P�ӵ�B��������ÿ��1����λ���ٶ����ű�BA���յ�A�˶�������PE�� ���P�˶���ʱ��Ϊt�룬��tΪ��ֵʱ����PAEΪ���������Σ�
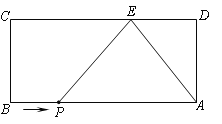
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���һ��P���߶�AC���ƶ�����AB��AC��5��BC��6����BP����СֵΪ________��
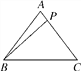
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ʵ��a��b��c����(a��![]() )2��
)2��![]() ��|c��2
��|c��2![]() |��0.
|��0.
(1)��a��b��c��ֵ��
(2)������a��b��cΪ���ܷ������Σ����ܹ��������Σ���������ε��ܳ�������������ܹ��������Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ھ���ABCD�У���B�Ľ�ƽ����BE��AD���ڵ�E����BED�Ľ�ƽ����EF��DC���ڵ�F����AB=9��DF=2FC����BC= �� ������������ţ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⷽ��
��1��2x+5=3
��2��6x��7=4x��5��
��3��4x+3��12��x��=6
��4��![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=�� ![]() x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B����Ϊ��6��0������C����Ϊ��0��6������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��
x2+bx+c��x�ύ�ڵ�A�͵�B����y�ύ�ڵ�C����B����Ϊ��6��0������C����Ϊ��0��6������D�������ߵĶ��㣬����D��x��Ĵ��ߣ�����ΪE������BD��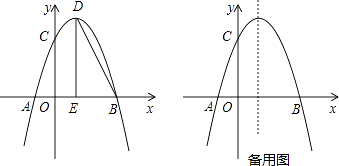
�����������ߵĽ���ʽ����D�����ꣻ
����F���������ϵĶ��㣬����FBA=��BDEʱ�����F�����ꣻ
��������M���������ϵĶ��㣬����M��MN��x���������߽��ڵ�N����P��x���ϣ���Q������ƽ���ڣ����߶�MNΪ�Խ�����������MPNQ����д����Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ĸ�������a��b��c��d��������������������ԣ�a��b���루c��d�������ǹ涨��
��a��b���c��d��=bc��ad��
���磺��1��2���3��4��=2��3��1��4=2��
���������涨����������⣺
��1���������ԣ�2����3���3����2��=�� ����
��2�����������ԣ���3��2x��1���1��x+1��=7����x=�� ����
��3���������ʽ����3��2x��1���k��x+k��=5+2k��x������ʱ��������k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
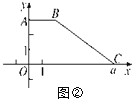
����Ŀ����ͼ�٣���ƽ��ֱ������ϵxOy�У���֪��A(0��3)��B(2��3)��OC��a.������ABCO��ֱ��y��x�۵�����A�����߶�OC�ϣ���Ӧ��ΪE.
(1)���E�����ꣻ
(2)����BC��AE����a��ֵ��(��ʾ��������ƽ�е��ı�����ƽ���ı��Σ�ƽ���ı��εĶԱ����)
����ͼ�ڣ�������ABCO�����Ϊ2a����ֱ��y��mx�������������Ϊ1��2�������֣���ֱ��y��mx�ĺ�������ʽ��
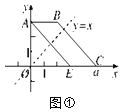
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com