
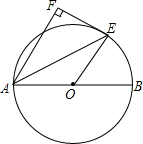
 如图,AB是⊙O的直径,AE是弦,EF是圆O的切线,E是切点,AF⊥EF,垂足是F,AE平分∠FAB吗?为什么?探索:你能探究出线段AE与AF、AB之间的关系吗?
如图,AB是⊙O的直径,AE是弦,EF是圆O的切线,E是切点,AF⊥EF,垂足是F,AE平分∠FAB吗?为什么?探索:你能探究出线段AE与AF、AB之间的关系吗? 分析 连接BE.先证明∠AEB=∠AFE=90°,然后利用同角的余角相等可知∠FEA=∠BEO,由∠OEB=∠OBE,可得到∠FEA=∠EBO,从而可证明△AFE∽AEB.
解答 解:连接BE.
∵AB是圆O的直径,
∴∠AEB=90°.
∴∠AEB=∠AFE.
∵EF是圆O的切线,
∴∠FEO=90°.
∵∠BEO+∠OEA=90°,∠OEA+∠AEF=90°,
∴∠FEA=∠BEO.
∵OE=OB,
∴∠OEB=∠OBE.
∴∠FEA=∠EBO.
∴△AFE∽AEB.
∴∠FAE=∠EAB.
∴AE是∠FAB的平分线.
∵△AFE∽AEB,
∴$\frac{AF}{AE}=\frac{AE}{AB}$.
∴AE2=AF•AB.
点评 本题主要考查的是切线的性质、相似三角形的性质和判定,证得△AFE∽AEB是解题的关键.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,A,B为某市中心的两座商场,分别在公路的两旁,由于人流量较大,经常堵塞,欲在公路上建一座立交桥PQ,缓解交通堵塞的情况,同时预防交通事故,则如何建立交桥PQ,使A到B的路程A→P→Q→B最短?要求立交桥PQ与公路垂直,并在图中画出路径.(公路两边a与b是平行的直线)
如图,A,B为某市中心的两座商场,分别在公路的两旁,由于人流量较大,经常堵塞,欲在公路上建一座立交桥PQ,缓解交通堵塞的情况,同时预防交通事故,则如何建立交桥PQ,使A到B的路程A→P→Q→B最短?要求立交桥PQ与公路垂直,并在图中画出路径.(公路两边a与b是平行的直线)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题
测量员在测量一块地时,先从点A向北偏东30°走100m到点B,再从点B向北偏西60°走80m到点C,又从点C向南偏西30°走60m到点D,最后以最短的距离回到A,试回答下列问题查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com