
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=-![]() 的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.
的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.
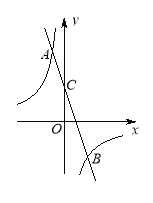
(1)求一次函数的解析式;
(2)点P是x轴上一点,且△BOP的面积是△BOC面积的2倍,求点P的坐标.
【答案】(1)、y=-3x+3;(2)、(4,0)或(-4,0)
【解析】
试题分析:(1)、首先根据反比例函数求出点A、B的坐标,然后将A、B的坐标代入一次函数解析式求出解析式;(2)、首先求出△BOC的面积,然后设点P的坐标为(a,0),根据面积求出a的值,得出点P的坐标.
试题解析:(1)∵ 点A(-1,m),B(n,-3)在反比例函数y=-![]() 的图象上,∴ m=6,n=2.
的图象上,∴ m=6,n=2.
∴A(-1,6),B(2,-3)
∵ 一次函数y=kx+b的图象过A(-1,6),B(2,-3)两点,
∴![]()
解得:![]()
∴ 一次函数的解析式为y=-3x+3.
(2)∵ 一次函数y=-3x+3与y轴交点C(0,3), 且B(2,-3)
∴△BOC面积为3.
∵P是x轴上一点,且△BOP的面积是△BOC面积的2倍,
∴ 设P(a,0),
∴ ![]() ,解得,a=±4
,解得,a=±4
∴ 点P的坐标为(4,0)或(-4,0).


科目:初中数学 来源: 题型:
【题目】某基地计划新建一个矩形的生物园地,一边靠旧墙(墙足够长),另外三边用总长54米的不锈钢栅栏围成,与墙平行的一边留一个宽为2米的出入口,如图所示,如何设计才能使园地的而积最大?下面是两位学生争议的情境:请根据上面的信息,解决问题:

(1)设AB=x米(x>0),试用含x的代数式表示BC的长;
(2)请你判断谁的说法正确,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过原点O及点A(-4,0)和点B(-6,3).
经过原点O及点A(-4,0)和点B(-6,3).
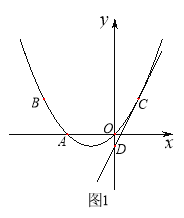
(1)求抛物线的解析式以及顶点坐标;
(2)如图1,将直线![]() 沿y轴向下平移后与(1)中所求抛物线只有一个交点C,平移后的直线与y轴交于点D,求直线CD的解析式;
沿y轴向下平移后与(1)中所求抛物线只有一个交点C,平移后的直线与y轴交于点D,求直线CD的解析式;
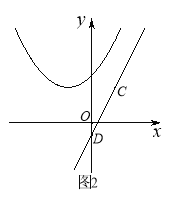
(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,请直接写出新抛物线上到直线CD距离最短的点的坐标及该最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据报道,至2008年5月1日零时,田湾核电站1、2号两台机组今年共累计发电42.96亿千瓦时.“42.96亿”用科学记数法可表示为__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a、b,如果ab<0,a+b<0.则下列各式成立的是( )
A. a<0,b<0 B. a>0,b<0且|b|<a
C. a<0,b>0且|a|<b D. a>0,b<0且|b|>a
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com