
【题目】已知抛物线![]() 经过原点O及点A(-4,0)和点B(-6,3).
经过原点O及点A(-4,0)和点B(-6,3).
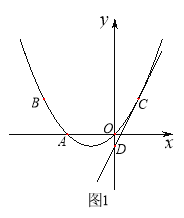
(1)求抛物线的解析式以及顶点坐标;
(2)如图1,将直线![]() 沿y轴向下平移后与(1)中所求抛物线只有一个交点C,平移后的直线与y轴交于点D,求直线CD的解析式;
沿y轴向下平移后与(1)中所求抛物线只有一个交点C,平移后的直线与y轴交于点D,求直线CD的解析式;
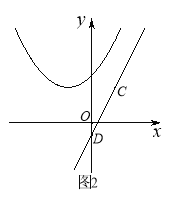
(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,请直接写出新抛物线上到直线CD距离最短的点的坐标及该最短距离.
【答案】(1)、y=![]() ,(-2,-1);(2)、y=2x-1;(3)、(2,7),
,(-2,-1);(2)、y=2x-1;(3)、(2,7),![]() .
.
【解析】
试题分析:(1)、利用待定系数法求出函数解析式,然后配成顶点式,得出顶点坐标;(2)、设直线的解析式为y=2x+m,然后和抛物线列出方程,根据跟的判别式求出m的值,得出解析式;(3)、根据题意得出最短距离以及点的坐标.
试题解析:(1)、∵ 抛物线经过![]() ,
,![]() ,
,![]() 三点,∴
三点,∴ 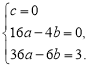 解得
解得 ![]()
∴ 抛物线的解析式为![]() .∵
.∵![]()
∴抛物线的顶点坐标为![]()
(2)、设直线CD的解析式为y=2x+m
根据题意,得![]() =2x+m,
=2x+m,
化简整理,得![]() -4x-4m=0,
-4x-4m=0,
由△=16+16m=0,解得m=-1,
∴直线CD的解析式为y=2x-1 .
(3)、点的坐标为(2,7),最短距离为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=-![]() 的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.
的图象交于A(-1,m),B(n,-3)两点,一次函数y=kx+b的图象与y轴交于点C.
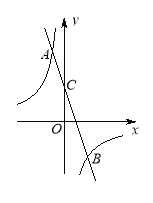
(1)求一次函数的解析式;
(2)点P是x轴上一点,且△BOP的面积是△BOC面积的2倍,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
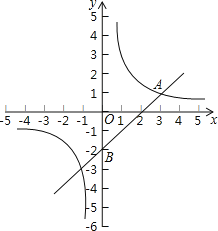
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com