
【题目】如图,在平面直角坐标系中,一次函数y=kx+b与反比例函数y=![]() (m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(m≠0)的图象交于点A(3,1),且过点B(0,﹣2).
(1)求反比例函数和一次函数的表达式;
(2)如果点P是x轴上一点,且△ABP的面积是3,求点P的坐标.
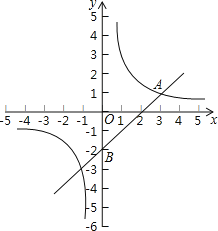
【答案】(1)y=![]() ;y=x-2;(2)(0,0)或(4,0)
;y=x-2;(2)(0,0)或(4,0)
【解析】试题分析:(1)利用待定系数法即可求得函数的解析式;
(2)首先求得AB与x轴的交点,设交点是C,然后根据S△ABP=S△ACP+S△BCP即可列方程求得P的横坐标.
试题解析:(1)∵反比例函数y=![]() (m≠0)的图象过点A(3,1),
(m≠0)的图象过点A(3,1),
∴3=![]()
∴m=3.
∴反比例函数的表达式为y=![]() .
.
∵一次函数y=kx+b的图象过点A(3,1)和B(0,-2).
∴![]() ,
,
解得: ![]() ,
,
∴一次函数的表达式为y=x-2;
(2)令y=0,∴x-2=0,x=2,
∴一次函数y=x-2的图象与x轴的交点C的坐标为(2,0).
∵S△ABP=3,
![]() PC×1+
PC×1+![]() PC×2=3.
PC×2=3.
∴PC=2,
∴点P的坐标为(0,0)、(4,0).


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径.半径OD垂直弦AC于点E.F是BA延长线上一点,![]() .
.
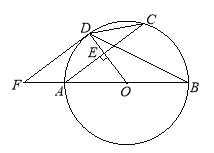
(1)判断DF与⊙O的位置关系,并证明;
(2)若AB=10,AC=8,求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过原点O及点A(-4,0)和点B(-6,3).
经过原点O及点A(-4,0)和点B(-6,3).
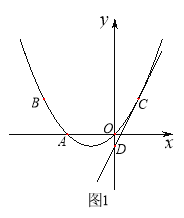
(1)求抛物线的解析式以及顶点坐标;
(2)如图1,将直线![]() 沿y轴向下平移后与(1)中所求抛物线只有一个交点C,平移后的直线与y轴交于点D,求直线CD的解析式;
沿y轴向下平移后与(1)中所求抛物线只有一个交点C,平移后的直线与y轴交于点D,求直线CD的解析式;
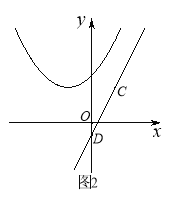
(3)如图2,将(1)中所求抛物线向上平移4个单位得到新抛物线,请直接写出新抛物线上到直线CD距离最短的点的坐标及该最短距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习“用直尺和圆规作射线OC,使它平分∠AOB”时,教科书介绍如下:

*作法:(1)以O为圆心,任意长为半径作弧,交OA于D,交OB于E;
(2)分别以D,E为圆心,以大于![]() DE的同样长为半径作弧,两弧交于点C ;
DE的同样长为半径作弧,两弧交于点C ;
(3)作射线OC.则OC就是所求作的射线.
小明同学想知道为什么这样做,所得到射线OC就是∠AOB的平分线.
小华的思路是连接DC、EC,可证△ODC≌△OEC,就能得到∠AOC=∠BOC. 其中证明△ODC≌△OEC的理由是_______________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于有理数a、b,如果ab<0,a+b<0.则下列各式成立的是( )
A. a<0,b<0 B. a>0,b<0且|b|<a
C. a<0,b>0且|a|<b D. a>0,b<0且|b|>a
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生产季节性产品的企业,当它的产品无利润时就会及时停产.现有一生产季节性产品的企业,其一年中获得的利润y和月份n之间函数关系式为y=-n2+14n-24,则该企业一年中利润最高的月份是( )
A. 5月 B. 6月 C. 7月 D. 8月
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com