
【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点 A作AG⊥BD分别交BD、BC于点G、E.
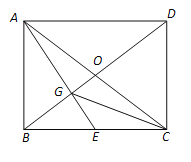
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
科目:初中数学 来源: 题型:
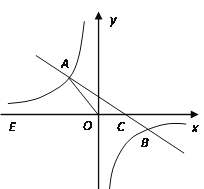
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
的图象交于二、四象限内的A、B两点,与x轴交于C点,点A的坐标为(- 3,4),点B的坐标为(6,n).
(1)求该反比例函数和一次函数的解析式;
(2)连接OB,求△AOB 的面积;
(3)在x轴上是否存在点P,使△APC是直角三角形. 若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB∥CD,直线l与直线AB,CD相交于点E,F,点P是射线EA上的一个动点(不包括端点E),将△EPF沿PF折叠,使顶点E落在点Q处.
⑴若∠PEF=48°,点Q恰好落在其中的一条平行线上,则∠EFP的度数为 .
⑵若∠PEF=75°,∠CFQ=![]() ∠PFC,求∠EFP的度数.
∠PFC,求∠EFP的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“绿水青山就是金山银山”,为保护生态环境,A,B两村准备各自清理所属区域养鱼网箱和捕鱼网箱,每村参加清理人数及总开支如下表:
村庄 | 清理养鱼网箱人数/人 | 清理捕鱼网箱人数/人 | 总支出/元 |
A | 15 | 9 | 57000 |
B | 10 | 16 | 68000 |
(1)若两村清理同类渔具的人均支出费用一样,求清理养鱼网箱和捕鱼网箱的人均支出费用各是多少元;
(2)在人均支出费用不变的情况下,为节约开支,两村准备抽调40人共同清理养鱼网箱和捕鱼网箱,要使总支出不超过102000元,且清理养鱼网箱人数小于清理捕鱼网箱人数,则有哪几种分配清理人员方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知A(a,b),B(2,2),且|a-b+8|+![]() =0.
=0.
(1)求点A的坐标;
(2)过点A作AC⊥x轴于点C,连接BC,AB,延长AB交x轴于点D,设AB交y轴于点E,那么OD与OE是否相等?请说明理由.
(3)在x轴上是否存在点P,使S△OBP=S△BCD?若存在,请求出P点坐标,若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,已EF=8,BE=3,CG=3,则图中阴影部分的面积是( )
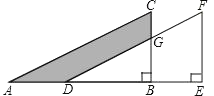
A.12.5B.19.5C.32D.45.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】母亲节过后,某校在本校学生中做了一次抽样调查,并把调查的结果分成三种类型:A. 不知道那一天是母亲节的;B. 知道但没有行动的;C. 知道并问候母亲的。如图是根据调查结果绘制的统计图(部分)。

(1)已知A类学生占被调查学生人数的![]() ,则被调查的学生共有多少人?
,则被调查的学生共有多少人?
(2)计算B类学生的人数并根据计算结果补全统计图;
(3)如果该校共有学生2000人,你估计这个学校学生中有多少人知道母亲节并问候了母亲。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.
(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
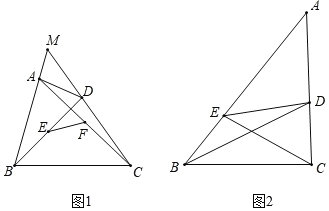
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com