
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.
(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
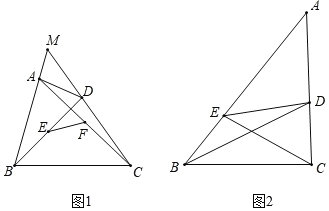
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
【答案】(1)如:平行四边形、矩形、菱形、等腰梯形等;(2)证明见解析;(3)①证明见解析;②四边形EBCD是等对边四边形.证明见解析.
【解析】
(1)理解等对边四边形的图形的定义,有平行四边形、矩形、菱形、等腰梯形等,可得出答案.
(2)取BC的中点N,连结EN,FN,由中位线定理可得EN=12CD,FN=12AB,可证明△EFN为等边三角形,则结论得证;
(3)①证明∠EOB=∠A,利用四边形内角和可证明∠BDC=∠AEC;
②作CG⊥BD于G点,作BF⊥CE交CE延长线于F点.根据AAS可证明△BCF≌△CBG,则BF=CG,证明△BEF≌△CDG,可得BE=CD,则四边形EBCD是“等对边四边形”.
(1)如:平行四边形、矩形、菱形、等腰梯形等.
(2)如图1,取BC的中点N,连结EN,FN,
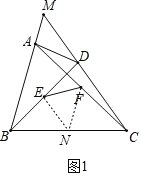
∴EN![]() CD,FN
CD,FN![]() AB,
AB,
∴EN=FN.
∵∠M=60°,
∴∠MBC+∠MCB=120°.
∵FN∥AB,EN∥MC,
∴∠FNC=∠MBC,∠ENB=∠MCB,
∴∠ENF=180°﹣120°=60°,
∴△EFN为等边三角形,
∴EF=FN![]() AB.
AB.
(3)①证明:∵∠BOE=∠BCE+∠DBC,∠DBC=∠ECB![]() ∠A,
∠A,
∴∠BOE=2∠DBC=∠A.
∵∠A+∠AEC+∠ADB+∠EOD=360°,∠BOE+∠EOD=180°,
∴∠AEC+∠ADB=180°.
∵∠ADB+∠BDC=180°,
∴∠BDC=∠AEC;
②解:此时存在等对边四边形,是四边形EBCD.
如图2,作CG⊥BD于G点,作BF⊥CE交CE延长线于F点.
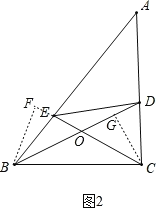
∵∠DBC=∠ECB![]() ∠A,BC=CB,∠BFC=∠BGC=90°,
∠A,BC=CB,∠BFC=∠BGC=90°,
∴△BCF≌△CBG(AAS),
∴BF=CG.
∵∠BEF=∠ABD+∠DBC+∠ECB,∠BDC=∠ABD+∠A,
∴∠BEF=∠BDC,
∴△BEF≌△CDG(AAS),
∴BE=CD,
∴四边形EBCD是等对边四边形.


科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD的两条对角线相交于点O,过点 A作AG⊥BD分别交BD、BC于点G、E.
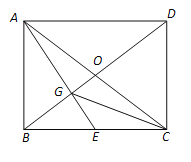
(1)求证:BE2=EGEA;
(2)连接CG,若BE=CE,求证:∠ECG=∠EAC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD的两条对角线相交于点O,点E是AB边的中点,图中已有三角形与△ADE面积相等的三角形(不包括△ADE)共有( )个.

A.3B.4C.5D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点B的坐标为(3,0),直线y=﹣x+3恰好经过B,C两点
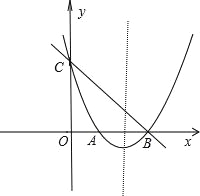
(1)写出点C的坐标;
(2)求出抛物线y=x2+bx+c的解析式,并写出抛物线的对称轴和点A的坐标;
(3)点P在抛物线的对称轴上,抛物线顶点为D且∠APD=∠ACB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将分别标有数字2,3,5的三张颜色、质地、大小完全一样的卡片背面朝上放在桌面上.
(1)随机抽取一张,求抽到奇数的概率;
(2)随机抽取一张作为个位上的数字(不放回),再抽取一张作为十位上的数字,能组成哪些两位数?并画树状图或列表求出抽取到的两位数恰好是35的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2 是关于x的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.
(1)求x1,x2 的值;
(2)若x1,x2 是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P是矩形ABCD对角线AC所在直线上的一个动点(点P不与点A,C重合),分别过点A,C向直线BP作垂线,垂足分别为点E,F,点O为AC的中点.

(1)如图1,当点P与点O重合时,请你判断OE与OF的数量关系;
(2)当点P运动到如图2所示位置时,请你在图2中补全图形并通过证明判断(1)中的结论是否仍然成立;
(3)若点P在射线OA上运动,恰好使得∠OEF=30°时,猜想此时线段CF,AE,OE之间有怎样的数量关系,直接写出结论不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校七年级甲、乙两班在参加全校演讲比赛的预选赛中,每班前![]() 名的成绩分别为:
名的成绩分别为:
甲班:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;乙班:
;乙班:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ;通过数据分析,列表如下:
;通过数据分析,列表如下:
班级 | 平均分 | 中位数 | 众数 | 方差 |
甲 |
|
|
|
|
乙 |
|
|
|
|
(1)直接写出表中![]() ,
,![]() ,
,![]() 的值;
的值;
(2)求![]() 的值,你认为哪个班前
的值,你认为哪个班前![]() 名同学的成绩较好?说明理由.
名同学的成绩较好?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
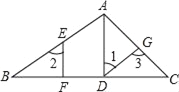
【题目】如图,在△ABC中,AD⊥BC,垂足为D,点E在AB上,EF⊥BC,垂足为F.
(1)AD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=115°,求∠BAC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com