
【题目】已知x1,x2 是关于x的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.
(1)求x1,x2 的值;
(2)若x1,x2 是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
【答案】(1)x1 = p,x2 = m + 2-p;
(2)当![]() 且m>-2时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为
且m>-2时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为![]() (或
(或![]() ).
).
【解析】试题分析:(1)化简方程,用分解因式法求出两根;
(2)直角三角形的面积为![]() x1x2,利用根与系数的关系可以得到关于p的关系式,然后利用二次函数可以求出什么时候有最大值.
x1x2,利用根与系数的关系可以得到关于p的关系式,然后利用二次函数可以求出什么时候有最大值.
试题解析:(1) 原方程变为:x2-(m + 2)x + 2m = p2-(m + 2)p + 2m,
∴ x2-p2-(m + 2)x +(m + 2)p = 0,
(x-p)(x + p)-(m + 2)(x-p)= 0,
即 (x-p)(x + p-m-2)= 0,
∴ x1 = p, x2 = m + 2-p.
(2)∵ 直角三角形的面积为![]() x1x2=
x1x2=![]() p(m+2-p)
p(m+2-p)
= ![]()
=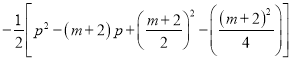
= ,
,
∴ 当![]() 且m>-2时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为
且m>-2时,以x1,x2为两直角边长的直角三角形的面积最大,最大面积为![]() (或
(或![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=90°,将△ABC沿AB方向平移AD的长度得到△DEF,已EF=8,BE=3,CG=3,则图中阴影部分的面积是( )
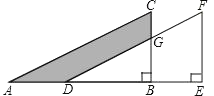
A.12.5B.19.5C.32D.45.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】目前![]() 节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
节能灯在城市已基本普及,为面向乡镇市场,苏宁电器分店决定用76000元购进室内用、室外用节能灯,已知这两种类型的节能灯进价、售价如下:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
室内用节能灯 | 40 | 58 |
室外用节能灯 | 50 | 70 |
(1)若该分店共购进节能灯1700盏,问购进的室内用、室外用节能灯各多少盏?
(2)若该分店将进货全部售完后获利要不少于32000元,问至少需要购进多少盏室内用节能灯?
(3)挂职锻炼的大学生村官王祥自酬了4650元在该分店购买这两种类型的节能灯若干盏,分发给村民使用,其中室内用节能灯盏数不少于室内用节能灯盏数的2倍,问王祥最多购买室外用节能灯多少盏?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD的度数为__________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:至少有一组对边相等的四边形为“等对边四边形”.
(1)请写出一个你学过的特殊四边形中是“等对边四边形”的名称;
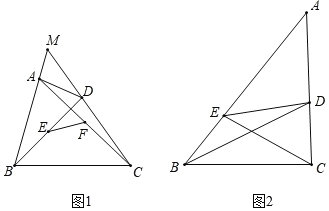
(2)如图1,四边形ABCD是“等对边四边形”,其中AB=CD,边BA与CD的延长线交于点M,点E、F是对角线AC、BD的中点,若∠M=60°,求证:EF![]() AB;
AB;
(3)如图2.在△ABC中,点D、E分别在边AC、AB上,且满足∠DBC=∠ECB![]() ∠A,线段CE、BD交于点.
∠A,线段CE、BD交于点.
①求证:∠BDC=∠AEC;
②请在图中找到一个“等对边四边形”,并给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在三角形![]() 中,点
中,点![]() 在线段
在线段![]() 上,
上,![]() 交
交![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,作直线
上,作直线![]() ,过点
,过点![]() 作直线
作直线![]() 交直线
交直线![]() 于点
于点![]() .
.
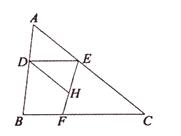
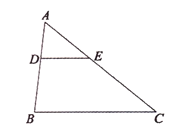
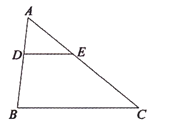
图1 图2 图3
(1)在如图1所示的情况下,求证:![]() ;
;
(2)若三角形![]() 不变,
不变,![]() ,
,![]() 两点的位置也不变,点
两点的位置也不变,点![]() 在直线
在直线![]() 上运动.
上运动.
①当点![]() 在三角形
在三角形![]() 内部时,说明
内部时,说明![]() 与
与![]() 的数量关系:
的数量关系:
②当点![]() 在三角形
在三角形![]() 外部时,①中结论是否依然成立?若不成立,
外部时,①中结论是否依然成立?若不成立,![]() 与
与![]() 又有怎样的数量关系?请在图2中画图探究,并说明理由.
又有怎样的数量关系?请在图2中画图探究,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题.
如图,在平面直角坐标系中,点D的坐标是(﹣3,1),点A的坐标是(4,3).
(1)点B和点C的坐标分别是________、________.
(2)将△ABC平移后使点C与点D重合,点A、B分别与点E、F重合,画出△DEF.并直接写出E点的坐标 ,F点的坐标 .
(3)若AB上的点M坐标为(x,y),则平移后的对应点M′的坐标为___ _____.
(4)求![]() 的面积.
的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数,
是常数, ![]() ).
).
(![]() )当该函数的图像与
)当该函数的图像与![]() 轴没有交点时,求
轴没有交点时,求![]() 的取值范围.
的取值范围.
(![]() )把该函数的图像沿
)把该函数的图像沿![]() 轴向上平移多少个单位长度后,得到的函数的图像与
轴向上平移多少个单位长度后,得到的函数的图像与![]() 轴只有一个公共点?
轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点D为△ABC边BC的延长线上一点.
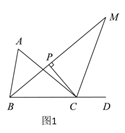
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证: ![]() ;
;
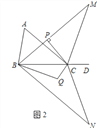
(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com