
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD的度数为__________度.

科目:初中数学 来源: 题型:
【题目】观察下列方程的特征及其解的特点.
①x+![]() =-3的解为x1=-1,x2=-2;
=-3的解为x1=-1,x2=-2;
②x+![]() =-5的解为x1=-2,x2=-3;
=-5的解为x1=-2,x2=-3;
③x+![]() =-7的解为x1=-3,x2=-4.
=-7的解为x1=-3,x2=-4.
解答下列问题:
(1)请你写出一个符合上述特征的方程为________,其解为________;
(2)根据这类方程的特征,写出第n个方程为________,其解为________;
(3)请利用(2)的结论,求关于x的方程x+![]() =-2(n+2)(其中n为正整数)的解.
=-2(n+2)(其中n为正整数)的解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红星期天从家里出发骑车去舅舅家做客,当她骑了一段路时,想起要买个礼物送给表弟,于是又折回到刚经过的一家商店,买好礼物后又继续骑车去舅舅家,以下是她本次去舅舅家所用的时间与路程的关系式示意图.根据图中提供的信息回答下列问题:
(1)小红家到舅舅家的路程是______米,小红在商店停留了______分钟;
(2)在整个去舅舅家的途中哪个时间段小红骑车速度最快,最快的速度是多少米/分
(3)本次去舅舅家的行程中,小红一共行驶了多少米?一共用了多少分钟?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】依据国家实行的《国家学生体质健康标准》,对怀柔区初一学生身高进行抽样调查,以便总结怀柔区初一学生现存的身高问题,分析其影响因素,为学生的健康发展及学校体育教育改革提出合理项建议.已知怀柔区初一学生有男生840人,女生800人,他们的身高在![]() 范围内,随机抽取初一学生进行抽样调查。抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表;
范围内,随机抽取初一学生进行抽样调查。抽取的样本中,男生比女生多2人,利用所得数据绘制如下统计图表;


根据统计图表提供的信息,下列说法中
①抽取男生的样本中,身高![]() 之间的学生有18人;
之间的学生有18人;
②初一学生中女生的身高的中位数在![]() 组;
组;
③抽取的样本中抽取女生的样本容量是38;
④初一学生身高在![]() 之间的学生约有800人。其中合理的是( )
之间的学生约有800人。其中合理的是( )
A. ①②B. ①④C. ②④D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+bx+c与y轴交于点C,与x轴交于A,B两点,点B的坐标为(3,0),直线y=﹣x+3恰好经过B,C两点
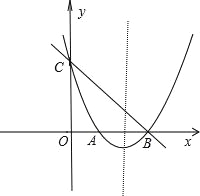
(1)写出点C的坐标;
(2)求出抛物线y=x2+bx+c的解析式,并写出抛物线的对称轴和点A的坐标;
(3)点P在抛物线的对称轴上,抛物线顶点为D且∠APD=∠ACB,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图1,DE∥AB,DF∥AC.
(1)求证:∠A=∠EDF.
(2)点G是线段AC上的一点,连接FG,DG.
①若点G是线段AE的中点,请你在图2中补全图形,判断∠AFG,∠EDG,∠DGF之间的数量关系,并证明.
②若点G是线段EC上的一点,请你直接写出∠AFG,∠EDG,∠DGF之间的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x1,x2 是关于x的方程(x-2)(x-m)=(p-2)(p-m)的两个实数根.
(1)求x1,x2 的值;
(2)若x1,x2 是某直角三角形的两直角边的长,问当实数m,p满足什么条件时,此直角三角形的面积最大?并求出其最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动点P在□ABCD边上沿着![]() 的方向匀速移动,到达点
的方向匀速移动,到达点![]() 时停止移动.已知P的速度为
时停止移动.已知P的速度为![]() 个单位长度/
个单位长度/![]() ,其所在位置用点
,其所在位置用点![]() 表示,
表示,![]() 到对角线
到对角线![]() 的距离(即垂线段
的距离(即垂线段![]() 的长)为
的长)为![]() 个单位长度,其中
个单位长度,其中![]() 与
与![]() 的函数图像如图②所示.
的函数图像如图②所示.
(1)若a=3,求当t=8时△BPQ的面积;
(2)如图②,点M,N分别在函数第一和第三段图像上,线段![]() 平行于横轴,
平行于横轴,![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() 、
、![]() .设
.设![]() 、
、![]() 时点P走过的路程分别为
时点P走过的路程分别为![]() 、
、![]() ,若
,若![]() +
+![]() =16,求
=16,求![]() 、
、![]() 的值.
的值.
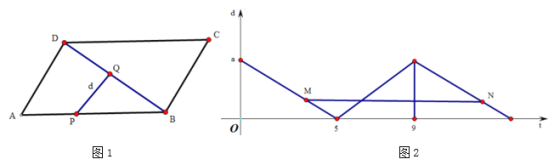
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
(1)在图1中,你发现线段AC,BD的数量关系是 ,直线AC,BD相交成 度角.
(2)将图1中的△OAB绕点O顺时针旋转90°角,这时(1)中的两个结论是否成立?请做出判断并说明理由.
(3)将图1中的△OAB绕点O顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com