
【题目】如图1,两个不全等的等腰直角三角形OAB和OCD叠放在一起,并且有公共的直角顶点O.
(1)在图1中,你发现线段AC,BD的数量关系是 ,直线AC,BD相交成 度角.
(2)将图1中的△OAB绕点O顺时针旋转90°角,这时(1)中的两个结论是否成立?请做出判断并说明理由.
(3)将图1中的△OAB绕点O顺时针旋转一个锐角,得到图3,这时(1)中的两个结论是否成立?请作出判断并说明理由.

【答案】(1)AC=BD,90;
(2)成立,理由见解析;
(3)成立,理由见解析.
【解析】试题分析:(1)由图可知线段AC,BD相等,且直线AC,BD相交成90°角.(2)以上关系仍成立.延长CA交BD于点E,根据勾股定理可证得AC=BD,即可证明△AOC≌△BOD,根据两全等三角形对应角的关系,即可证明CE⊥BD.(3)结论仍成立.延长CA交OD于E,交BD于F,可证得△COA≌△DOB,同上即可得结论.
试题解析:(1)在图1中,线段AC,BD的数量关系是相等,直线AC,BD相交成90度角;
(2)(1)中结论仍成立;
证明如下:如图延长CA交BD于点E,
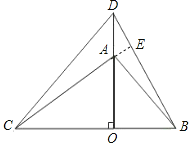
∵等腰直角三角形OAB和OCD,
∴OA=OB,OC=OD,
∵AC2=AO2+CO2,BD2=OD2+OB2,
∴AC=BD;
∴△DOB≌△COA(SSS),
∴∠CAO=∠DBO,∠ACO=∠BDO,
∵∠ACO+∠CAO=90°,
∴∠ACO+∠DBO=90°,则∠AEB=90°,即直线AC,BD相交成90°角。
(3)结论仍成立;如图延长CA交OD于E,交BD于F,
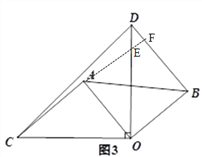
∵∠COD=∠AOB=90°,
∴∠COA+∠AOD=∠AOD+∠DOB,
即:∠COA=∠DOB,
∵CO=OD,OA=OB,
∴△COA≌△DOB(SAS),
∴AC=BD,∠ACO=∠ODB;
∵∠CEO=∠DEF,
∴∠COE=∠EFD=90°,
∴AC⊥BD,即直线AC,BD相交成90°角。


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D,∠ACD=3∠BCD,E是斜边AB的中点,则∠ECD的度数为__________度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() 是常数,
是常数, ![]() ).
).
(![]() )当该函数的图像与
)当该函数的图像与![]() 轴没有交点时,求
轴没有交点时,求![]() 的取值范围.
的取值范围.
(![]() )把该函数的图像沿
)把该函数的图像沿![]() 轴向上平移多少个单位长度后,得到的函数的图像与
轴向上平移多少个单位长度后,得到的函数的图像与![]() 轴只有一个公共点?
轴只有一个公共点?
查看答案和解析>>
科目:初中数学 来源: 题型:
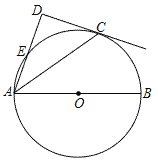
【题目】如图,点C在以AB为直径的⊙O上,AD与过点C的切线垂直,垂足为点D,AD交⊙O于点E.
(1) 求证:AC平分∠DAB;
(2) 连接BE交AC于点F,若cos∠CAD=![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中国传统节日“端午节”的临近,永旺超市决定开展“欢度端午,回馈顾客”的让利促销活动,对部分品牌粽子进行打折销售,其中甲品牌粽子打八折,乙品牌粽子打七五折.已知打折前,买1盒甲品牌粽子和2盒乙品牌粽子需230元;打折后,买50盒甲品牌粽子和40盒乙品牌粽子需要5200元.
(1)打折前甲、乙两种品牌粽子每盒分别为多少元?
(2)阳光敬老院需购买甲品牌粽子80盒,乙品牌粽子100盒,问打折后购买这批粽子比不打折节省了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解初三年级1000名学生的身体健康情况,从该年级随机抽取了若干名学生,将他们按体重(均为整数,单位:kg)分成五组(A:39.5~46.5;B:46.5~53.5;C:53.5~60.5;D:60.5~67.5;E:67.5~74.5),并依据统计数据绘制了如下两幅尚不完整的统计图.

解答下列问题:
(1)这次抽样调查的样本容量是 ,并补全频数分布直方图;
(2)C组学生的频率为 ,在扇形统计图中D组的圆心角是 度;
(3)请你估计该校初三年级体重超过60kg的学生大约有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点D为△ABC边BC的延长线上一点.
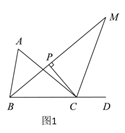
(1)若∠A∶∠ABC=3∶4,∠ACD=140°,求∠A的度数;
(2)若∠ABC的角平分线与∠ACD的角平分线交于点M,过点C作CP⊥BM于点P.
求证: ![]() ;
;
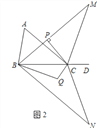
(3)在(2)的条件下,将△MBC以直线BC为对称轴翻折得到△NBC,∠NBC的角平分线与∠NCB的角平分线交于点Q(如图2),试探究∠BQC与∠A有怎样的数量关系,请写出你的猜想并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC绕直角顶点A,沿顺时针方向旋转后得到Rt△AB1C1,当点B1恰好落在斜边BC的中点时,则∠B1AC=( )

A.25°B.30°C.40°D.60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为鼓励市民节约用电,小亮家所在地区规定:每户居民如果一个月的用电量不超过![]() 度,那么这户居民这个月只需交
度,那么这户居民这个月只需交![]() 元电费;如果超过
元电费;如果超过![]() 度,则这个月除了仍要交
度,则这个月除了仍要交![]() 元的电费以外,超过的部分还要按每度
元的电费以外,超过的部分还要按每度![]() 元交电费.已知小亮家
元交电费.已知小亮家![]() 月份用电
月份用电![]() 度,交电费
度,交电费![]() 元;
元;![]() 月份用电
月份用电![]() 度,交电费
度,交电费![]() 元.
元.
(1)请直接写出小亮家![]() 月份超过
月份超过![]() 度部分的用电量(用含
度部分的用电量(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com