
 回答下列问题:
回答下列问题:分析 (1)由于点M是AC中点,所以MC=$\frac{1}{2}$AC,由于点N是BC中点,则CN=$\frac{1}{2}$BC,而MN=MC+CN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB,从而可以求出MN的长度;
(2)由于点M是AC中点,所以MC=$\frac{1}{2}$AC,由于点N是BC中点,则CN=$\frac{1}{2}$BC,而MN=MC-CN=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$AB,从而可以求出MN的长度;
(3)根据M为AC的中点,N为BC的中点,于是得到CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,然后根据线段和差即可得到结论.
解答 解:(1)∵点M是AC中点,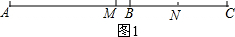
∴MC=$\frac{1}{2}$AC,
∵点N是BC中点,
∴CN=$\frac{1}{2}$BC,
∴MN=MC+CN=$\frac{1}{2}$(AC+BC)=$\frac{1}{2}$AB=4cm;
(2)如图1,∵点M是AC中点,
∴MC=$\frac{1}{2}$AC,
∵点N是BC中点,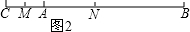
∴CN=$\frac{1}{2}$BC,
∴MN=MC-CN=$\frac{1}{2}$(AC-BC)=$\frac{1}{2}$AB=4cm;
(3)如图2,
∵M为AC的中点,N为BC的中点,
∴CM=$\frac{1}{2}$AC,CN=$\frac{1}{2}$BC,
∴MN=CN-CM=$\frac{1}{2}$BC-$\frac{1}{2}$AC=$\frac{1}{2}$(BC-AC)=$\frac{1}{2}$AB=4cm.
点评 本题考查的是两点间的距离,熟知各线段之间的和、差及倍数关系是解答此题的关键.


科目:初中数学 来源: 题型:选择题
| A. | $\left\{\begin{array}{l}{x+y=78}\\{3x+2y=30}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+y=78}\\{2x+3y=30}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+y=30}\\{2x+3y=78}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x+y=30}\\{3x+2y=78}\end{array}\right.$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 675×102 | B. | 6.75×104 | C. | 6.75×105 | D. | 0.675×105 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
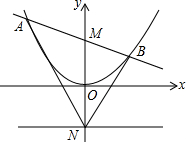 如图所示,已知抛物线y=$\frac{1}{4}$x2,点M、N的坐标分别为(0,1)、(0,-1).
如图所示,已知抛物线y=$\frac{1}{4}$x2,点M、N的坐标分别为(0,1)、(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a=$\frac{1}{3}$ | B. | a=-2 | C. | a=1 | D. | a=$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com