
【题目】在平面直角坐标系中,抛物线C1:y=ax2+4x+4a(0<a<2)
(1)当C1与x轴有唯一一个交点时,求此时C1的解析式;
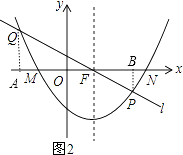
(2)如图①,若A(1,yA),B(0,yB),C(﹣1,yC)三点均在C1上,连BC作AE∥BC交抛物线C1于E,求点E到y轴的距离;
(3)若a=1,将抛物线C1先向右平移3个单位,再向下平移2个单位得到抛物线C2 , 如图②,抛物线C2与x轴相交于点M、N(M点在N点的左边),抛物线的对称轴交x轴于点F,过点F的直线l与抛物线C2相交于P,Q(P在第四象限)且S△FMQ=2S△FNP , 求直线l的解析式.
【答案】
(1)
解:根据题意得△=42﹣4a4a=0,解得a1=1,a2=﹣1,
而0<a<2,
所以a=1,
所以此时C1的解析式为y=x2+4x+4;
(2)
解:根据题意得A(1,5a+4),B(0,4a),C(﹣1,5a﹣4),
设直线BC的解析式为y=kx+4a,
把C(﹣1,5a﹣4)代入得﹣k+4a=5a﹣4,解得k=4﹣a,
∴直线BC的解析式为y=(4﹣a)x+4a,
∵BC∥AE,
∴AE的解析式可设为y=(4﹣a)x+n,
把A(1,5a+4)代入得4﹣a+n=5a+4,解得n=6a,
∴直线AE的解析式为y=(4﹣a)x+6a,
方程组 ![]() 消去y得x2+x﹣2=0,解得x1=1,x2=﹣2,
消去y得x2+x﹣2=0,解得x1=1,x2=﹣2,
∴E点的横坐标为﹣2,
∴点E到y轴的距离为2;
(3)
解:作QA⊥x轴于A,PB⊥x轴于B,如图,
当a=1时,y=x2+4x+4=(x+2)2,抛物线C1的顶点坐标为(﹣2,0),把点(﹣2,0)先向右平移3个单位,再向下平移2个单位得到对应点的坐标为(1,﹣2),
所以抛物线C2的解析式为y=(x﹣1)2﹣2,即y=x2﹣2x﹣1,则抛物线的对称轴为直线x=1,所以F(1,0)
∵抛物线C2与x轴相交于点M、N(M点在N点的左边),
∴FM=FN,
∵S△FMQ=2S△FNP,
∴QA=2PB,
∵AQ∥PB,
∴ ![]() =2,即FA=2BF,
=2,即FA=2BF,
设P(t,t2﹣2t﹣1),则BF=t﹣1,
∴AF=2(t﹣1),
∴OA=2(t﹣1)﹣1=2t﹣3,
∴Q[3﹣2t,(3﹣2t)2﹣2(3﹣2t)﹣1]
∴(3﹣2t)2﹣2(3﹣2t)﹣1=﹣2(t2﹣2t﹣1),
整理得t2﹣2t=0,解得t1=0(舍去),t2=2,
∴P(2,﹣1),Q(﹣1,2),
设直线PQ的解析式为y=px+q,
把P(2,﹣1),Q(﹣1,2)代入得 ![]() ,解得
,解得 ![]() ,
,
∴直线l的解析式为y=﹣x+1.
【解析】(1)根据△的意义和抛物线与x轴的交点问题得△=42﹣4a4a=0,然后解方程求出满足条件的a的值,从而得到此时C1的解析式;(2)先用a表示出A(1,5a+4),B(0,4a),C(﹣1,5a﹣4),再利用待定系数法得到直线BC的解析式为y=(4﹣a)x+4a,根据两直线平行问题,AE的解析式可设为y=(4﹣a)x+n,则把A(1,5a+4)代入得n=6a,所以直线AE的解析式为y=(4﹣a)x+6a,通过解方程组 ![]() 可得E点和A点坐标,消去y得x2+x﹣2=0,然后解方程求出x即可得到E点的横坐标,从而得到点E到y轴的距离;(3)作QA⊥x轴于A,PB⊥x轴于B,如图,当a=1时,y=(x+2)2 , 则抛物线C1的顶点坐标为(﹣2,0),利用抛物线的几何变换得到抛物线C2的解析式为y=(x﹣1)2﹣2,即y=x2﹣2x﹣1,F(1,0),利用抛物线的对称性得FM=FN,再利用三角形面积公式可得QA=2PB,利用平行线分线段成比例定理得FA=2BF,设P(t,t2﹣2t﹣1),则BF=t﹣1,AF=2(t﹣1),则OA=2(t﹣1)﹣1=2t﹣3,所以Q[3﹣2t,(3﹣2t)2﹣2(3﹣2t)﹣1],然后利用AQ=2PB得到(3﹣2t)2﹣2(3﹣2t)﹣1=﹣2(t2﹣2t﹣1),解得t1=0(舍去),t2=2,于是得到P(2,﹣1),Q(﹣1,2),最后利用待定系数法确定直线l的解析式.
可得E点和A点坐标,消去y得x2+x﹣2=0,然后解方程求出x即可得到E点的横坐标,从而得到点E到y轴的距离;(3)作QA⊥x轴于A,PB⊥x轴于B,如图,当a=1时,y=(x+2)2 , 则抛物线C1的顶点坐标为(﹣2,0),利用抛物线的几何变换得到抛物线C2的解析式为y=(x﹣1)2﹣2,即y=x2﹣2x﹣1,F(1,0),利用抛物线的对称性得FM=FN,再利用三角形面积公式可得QA=2PB,利用平行线分线段成比例定理得FA=2BF,设P(t,t2﹣2t﹣1),则BF=t﹣1,AF=2(t﹣1),则OA=2(t﹣1)﹣1=2t﹣3,所以Q[3﹣2t,(3﹣2t)2﹣2(3﹣2t)﹣1],然后利用AQ=2PB得到(3﹣2t)2﹣2(3﹣2t)﹣1=﹣2(t2﹣2t﹣1),解得t1=0(舍去),t2=2,于是得到P(2,﹣1),Q(﹣1,2),最后利用待定系数法确定直线l的解析式.
【考点精析】本题主要考查了二次函数的图象的相关知识点,需要掌握二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】宜兴科技公司生产销售一种电子产品,该产品总成本包括技术成本、制造成本、销售成本三部分,经核算,2013年该产品各部分成本所占比例约为2:a:1.且2013年该产品的技术成本、制造成本分别为400万元、1400万元.
(1)确定a的值,并求2013年产品总成本为多少万元;
(2)为降低总成本,该公司2014年及2015年增加了技术成本投入,确保这两年技术成本都比前一年增加一个相同的百分数m(m<50%),制造成本在这两年里都比前一年减少一个相同的百分数2m;同时为了扩大销售量,2015年的销售成本将在2013年的基础上提高10%,经过以上变革,预计2015年该产品总成本达到2013年该产品总成本的 ![]() ,求m的值.
,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】折叠矩形纸片ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,折痕AE的长( )
A. ![]() cm B.
cm B. ![]() cm C. 12cm D. 13cm
cm C. 12cm D. 13cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感,他惊喜的发现,当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明,下面是小聪利用图1证明勾股定理的过程:
将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°,求证:a2+b2=c2.
证明:连结DB,过点D作BC边上的高DF,则DF=EC=b﹣a,
∵S四边形ADCB=S△ACD+S△ABC= 12 b2+ 12 ab.
又∵S四边形ADCB=S△ADB+S△DCB= 12 c2+ 12 a(b﹣a)
∴ 12 b2+ 12 ab= 12 c2+ 12 a(b﹣a)
∴a2+b2=c2
请参照上述证法,利用图2完成下面的证明.
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.求证:a2+b2=c2 .

查看答案和解析>>
科目:初中数学 来源: 题型:
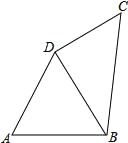
【题目】如图,在四边形ABCD中,AB=AD=8,∠A=60°,∠ADC=150°,四边形ABCD的周长为32.
(1)求∠BDC的度数;
(2)四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠ACB=90°,AC=BC,BD⊥DE,AE⊥DE,垂足分别为D、E.(这几何模型具备“一线三直角”)如下图:
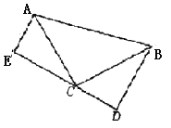
(1)①请你证明:△ACE≌△CBD;②若AE=3,BD=5,求DE的长;
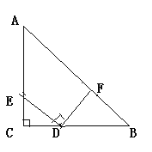
(2)迁移:如图:在等腰Rt△ABC中,且∠C=90°,CD=2,BD=3,D、E分别是边BC,AC上的点,将DE绕点D顺时针旋转90°,点E刚好落在边AB上的点F处,则CE=________。(不要求写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某瓜农采用大棚栽培技术种植了一亩地的良种西瓜,这亩地产西瓜600个,在西瓜上市前该瓜农随机摘下了10个成熟的西瓜,称重如下:
西瓜质量(单位:千克) | 5.4 | 5.3 | 5.0 | 4.8 | 4.4 | 4.0 |
西瓜数量(单位:个) | 1 | 2 | 3 | 2 | 1 | 1 |
(1)这10个西瓜质量的众数和中位数分别是 和 ;
(2)计算这10个西瓜的平均质量,并根据计算结果估计这亩地共可收获西瓜约多少千克?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b﹣3)2=0.
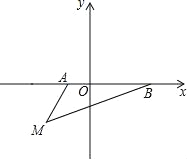
(1)填空:a= ,b= ;
(2)如果在第三象限内有一点M(﹣2,m),请用含m的式子表示△ABM的面积;
(3)在(2)条件下,当m=![]() 时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
时,在y轴上有一点P,使得△BMP的面积与△ABM的面积相等,请求出点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com