
【题目】如图,矩形ABCD中,AB=6,BC=4,过对角线BD中点O的直线分别交AB,CD边于点E,F.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,求EF的长.

【答案】(1)证明见解析.(2)![]() .
.
【解析】
试题分析:(1)根据平行四边形ABCD的性质,判定△BOE≌△DOF(ASA),得出四边形BEDF的对角线互相平分,进而得出结论;
(2)在Rt△ADE中,由勾股定理得出方程,解方程求出BE,由勾股定理求出BD,得出OB,再由勾股定理求出EO,即可得出EF的长.
试题解析:(1)证明:∵四边形ABCD是矩形,O是BD的中点,
∴∠A=90°,AD=BC=4,AB∥DC,OB=OD,
∴∠OBE=∠ODF,
在△BOE和△DOF中,
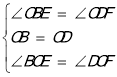 ,
,
∴△BOE≌△DOF(ASA),
∴EO=FO,
∴四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,BE⊥EF,
设BE=x,则 DE=x,AE=6﹣x,
在Rt△ADE中,DE2=AD2+AE2,
∴x2=42+(6﹣x)2,
解得:x=![]() ,
,
∵BD=![]() ,
,
∴OB=![]() BD=
BD=![]() ,
,
∵BD⊥EF,
∴EO=![]() ,
,
∴EF=2EO=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1 , 如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1 , 使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 . 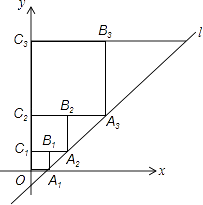
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【知识链接】 有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.
例如: ![]() 的有理化因式是
的有理化因式是 ![]() ;1﹣
;1﹣ ![]() 的有理化因式是1+
的有理化因式是1+ ![]() .
.
分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到化去分母中根号的目的.如:![]() =
= ![]() =
= ![]() ﹣1,
﹣1, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() .
.
(1)【知识理解】 填空:2 ![]() 的有理化因式是;
的有理化因式是;
直接写出下列各式分母有理化的结果:
① ![]() =;②
=;② ![]() = .
= .
(2)【启发运用】 计算: ![]() +
+ ![]() +
+ ![]() +…+
+…+ ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+4的图象与x轴交于点B(-2,0),点C(8,0),与y轴交于点A.
(1)求二次函数y=ax2+bx+4的表达式;
(2)连接AC,AB,若点N在线段BC上运动(不与点B,C重合),过点N作NM∥AC,交AB于点M,当△AMN面积最大时,求N点的坐标;
(3)连接OM,在(2)的结论下,求OM与AC的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某港口P位于东西方向的海岸线上“远航”号、“海天”号轮船同时离开港口,各自沿同定方向航行,“远航”号每小时航行16n mile,“海天”号每小时航行12n mile,它们离开港口一个半小时后分别位于点Q,R处,且相距30n mile 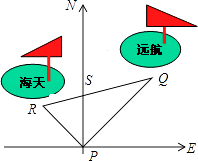
(1)求PQ,PR的长度;
(2)如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com