
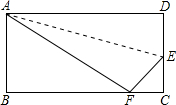
 把长AD=10cm,宽AB=6cm的矩形沿着AE对折,使点D落在BC边的点F上,则DE=$\frac{10}{3}$.
把长AD=10cm,宽AB=6cm的矩形沿着AE对折,使点D落在BC边的点F上,则DE=$\frac{10}{3}$. 分析 在△ABF中,利用折叠及勾股定理易得BF长度,即可得CF的长度,用DE表示出EC,利用Rt△EFC的三边关系即可求得DE长度.
解答 解:由折叠的性质知,DE=EF,AF=AD=10cm,
在Rt△ABF中,由勾股定理知,BF=8cm,FC=BC-BF=10-8=2cm,
在Rt△EFC中,由勾股定理知,FC2+CE2=EF2,
(6-DE)2+22=EF2,
解得EF=DE=$\frac{10}{3}$cm.
故答案为:$\frac{10}{3}$,
点评 此题主要考查了折叠的性质、矩形的性质,勾股定理等知识点.利用折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等得出是解题关键.


科目:初中数学 来源: 题型:选择题
| 时刻 | 12:00 | 13:00 | 14:30 |
| 碑上 的数 | 是一个两位数,数字之和为6 | 十位与个位数字与12:00时所看到的正好颠倒了 | 比12:00时看到的两位数中间多了个0 |
| A. | 24 | B. | 42 | C. | 51 | D. | 15 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
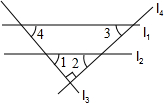 如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )
如图,直线l1∥l2,l3⊥l4,有下列三个命题,①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4,则( )| A. | 只有①正确 | B. | 只有②正确 | C. | ①和③正确 | D. | ①②③都正确 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )
一只小鸟自由自在地在空中飞行,然后随意落在如图所示的某个方格中(每个方格除颜色外完全一样),那么小鸟停在黑色方格中的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{7}{12}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )
小萍要在一幅长60cm、宽40cm的风景画的四周外围,镶上一条宽度相同的金色纸边,制成一幅挂画(如图),使风景画的面积是整幅挂图面积54%.设金色纸边的宽为xcm,根据题意所列方程为( )| A. | (60+x)(40+x)×54%=60×40 | B. | (60+2x)(40+2x)×54%=60×40 | ||
| C. | (60+2x)(40+2x)=60×40×54% | D. | (60+x)(40+x)=60×40×54% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| n | 60° | 72° | 90° | 120° |
| R关于r的函数解析式 | 6r | 5r | 4r | 3r |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com