
【题目】制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800 ℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃,煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图),已知该材料初始温度是26 ℃.
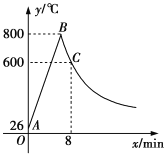
(1)分别求出材料煅烧和锻造时y关于x的函数解析式,并写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于400℃时,须停止操作,那么锻造的操作时间有多长?
【答案】(1)材料煅烧时:![]() ,锻造时:
,锻造时:![]() ;(2)锻造的操作时间有6min
;(2)锻造的操作时间有6min
【解析】
(1)首先根据题意,材料煅烧时,温度y与时间x成一次函数关系;锻造操作时,温度y与时间x成反比例关系,将题中数据代入用待定系数法可得两个函数的关系式;
(2)把y=480代入![]() 中,进一步求解可得答案.
中,进一步求解可得答案.
解:(1)设材料锻造时y关于x的函数解析式为![]() ,将点C(8,600)代入得,
,将点C(8,600)代入得,
![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,
,
∴点B的坐标为(6,800),锻造时y关于x的函数解析式为![]() .
.
设材料煅烧时y关于x的函数解析式为![]() ,将点A(0,26),点B(6,800)代入得,
,将点A(0,26),点B(6,800)代入得,
![]() ,解得
,解得![]() ,
,
∴材料煅烧时y关于x的函数解析式为![]() .
.
(2)把![]() 代入
代入![]() ,得
,得![]() ,
,
![]() ,
,
∴锻造的操作时间有6min.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.调查全校建档立卡户学生的人数,宜采用抽样调查
B.随机抽取某班7名学生的数学成绩:105,102,105,113,116,105,119,则数据的中位数和众数都是105
C.通过对甲、乙两组学生数学成绩的跟踪调查,整理得知两组数据的方差分别为:![]() =0.123,
=0.123,![]() =0.362,则乙组数据比甲组数据稳定
=0.362,则乙组数据比甲组数据稳定
D.必然事件发生的概率为1,随机事件发生的概率为0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,四边形ACDE是平行四边形,连结CE交AD于点F,连结BD交CE于点G,连结BE. 下列结论中:① CE=BD; ②△ADC是等腰直角三角形;
③∠ADB=∠AEB; ④ CD·AE=EF·CG;
一定正确的结论有
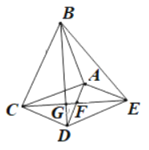
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() .点
.点![]() 从
从![]() 出发以每秒2个单位长度的速度向
出发以每秒2个单位长度的速度向![]() 运动;点
运动;点![]() 从
从![]() 同时出发,以每秒1个单位长度的速度向
同时出发,以每秒1个单位长度的速度向![]() 运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点
运动.其中一个动点到达终点时,另一个动点也随之停止运动.过点![]() 作
作![]() 垂直
垂直![]() 轴于点
轴于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,连接
,连接![]() .
.
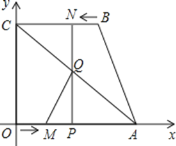
(1) 求![]() 的面积
的面积![]() 与运动时间
与运动时间![]() 的函数关系式, 并写出自变量
的函数关系式, 并写出自变量![]() 的取值范围, 当
的取值范围, 当![]() 为何值时,
为何值时,![]() 的值最大?
的值最大?
(2)是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
(3) 当![]() 为以
为以![]() 为底的等腰三角形时,求
为底的等腰三角形时,求![]() 值.
值.
(4) 是否存在这样的![]() 值,使直线
值,使直线![]() 将
将![]() 的周长和面积同时平分?若存在,求出
的周长和面积同时平分?若存在,求出![]() 值,若不存在,说明理由.
值,若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3.
(1)求它的对称轴和顶点坐标;
(2)求该抛物线与x轴的交点坐标;
(3)建立平面直角坐标系,画出这条抛物线的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线C1:y1=a(x﹣h)2+2,直线1:y2=kx﹣kh+2(k≠0).
(1)求证:直线l恒过抛物线C的顶点;
(2)若a>0,h=1,当t≤x≤t+3时,二次函数y1=a(x﹣h)2+2的最小值为2,求t的取值范围.
(3)点P为抛物线的顶点,Q为抛物线与直线l的另一个交点,当1≤k≤3时,若线段PQ(不含端点P,Q)上至少存在一个横坐标为整数的点,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧![]() 上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是
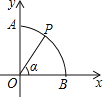
A. (sinα,sinα) B. (cosα,cosα) C. (cosα,sinα) D. (sinα,cosα)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com