
【题目】在平面直角坐标系xOy中,抛物线y=ax2-2ax-3a (a<0)经过点A(-1,0),将点B(0,4)向右平移5个单位长度,得到点C.
(1)求点C的坐标;
(2)求抛物线的对称轴;
(3)若抛物线与线段BC恰有一个公共点,结合函数图像,求a的取值范围.
【答案】(1)C(5,4);(2)x=1; (3) ![]() 或
或![]()
【解析】
(1)根据坐标平移的特点是左减右加、上加下减可以求得点C的坐标;
(2)根据抛物线C1:y=ax2﹣2ax﹣3a(a≠0)可以求得该抛物线的对称轴;
(3)分三种情况讨论:①当抛物线顶点在线段BC上时,②当抛物线与直线BC的左交点在B的左边,右交点在线段BC上时,③当抛物线与直线BC的左交点在线段BC上,右交点在线段BC的延长线上时.
(1)∵点B(0,4)向右平移5个单位长度,得到点C,
∴点C的坐标为(5,4);
(2)∵抛物线C1:y=ax2﹣2ax﹣3a,
∴对称轴是直线x=﹣![]() =1;
=1;
(3)∵y=ax2﹣2ax﹣3a=a(x-1)2﹣4a,
∴分三种情况讨论:
①当抛物线顶点在线段BC上时,抛物线与线段BC只有一个交点,此时﹣4a=4,
解得:a=-1;
②当抛物线与直线BC的左交点在B的左边,右交点在线段BC上时,抛物线与线段BC只有一个交点,此时抛物线与y轴的交点在点B上方,
∴-3a>4,
解得:a<![]() .
.
③当抛物线与直线BC的左交点在线段BC上,右交点在线段BC的延长线上时,抛物线与线段BC只有一个交点.
∵抛物线开口向下,此时抛物线与x轴的右交点的横坐标一定大于5,这与抛物线一定过(-1,0)和(3,0)矛盾,此种情况不成立.
综上所述:a的取值范围是![]() 或a=-1.
或a=-1.



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
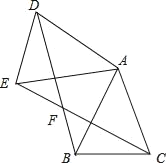
(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中, A(0,2),B(-1,0),Rt△AOC的面积为4.
(1)求点C的坐标;
(2)抛物线![]() 经过A、B、C三点,求抛物线的解析式和对称轴;
经过A、B、C三点,求抛物线的解析式和对称轴;
(3)设点P(m,n)是抛物线在第一象限部分上的点,△PAC的面积为S,求S关于m的函数关系式,并求使S最大时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作图题:(保留作图痕迹,不写做法)
(1)已知:如图,四边形ABCD与四边形EFGH成中心对称,试画出它们的对称中心O。
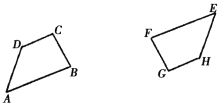
(2)考古学家在考古过程中发现一个圆盘,但是因为历史悠久,已经有一部分缺失,如图所示.现希望复原圆盘,需要先找到圆盘的圆心,才能继续完成后续修复工作.请利用直尺(无刻度)和圆规,在图中找出圆心O.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级(1)班部分学生接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了如图①②两幅不完整的统计图,请根据图中的信息解答下列问题.
(1)九年级(1)班接受调查的学生共有多少名?
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为________米.
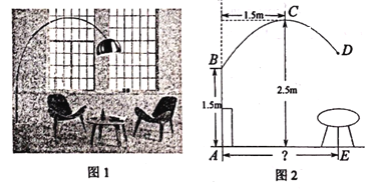
查看答案和解析>>
科目:初中数学 来源: 题型:
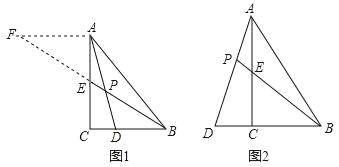
【题目】在△ABC中,∠ACB=90°,BE是AC边上的中线,点D在射线BC上.
发现:如图1,点D在BC边上,CD:BD=1:2,AD与BE相交于点P,过点A作AF∥BC,交BE的延长线于点F,求![]() 的值为.
的值为.
解决问题:如图2,在△ABC中,∠ACB=90°,点D在BC的延长线上,AD与AC边上的中线BE的延长线交于点P,DC:BC=1:2.求![]() 的值.
的值.
应用:若CD=2,AC=6,求BP的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com