练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．下列所述的图形中，既是轴对称图形，又是中心对称图形的是（　　）
    A．平行四边形B．等腰直角三角形C．菱形D．正五边形

    分析 根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．

    解答 解：A、平行四边形不是轴对称图形，是中心对称图形，故本选项错误；
    B、等腰直角三角形是轴对称图形，不是中心对称图形，故本选项错误；
    C、菱形既是轴对称图形，又是中心对称图形，故本选项正确；
    D、正五边形是轴对称图形，不是中心对称图形，故本选项错误．
    故选C．

    点评 本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．已知抛物线y=$\frac{1}{2}$x2-nx+$\frac{1}{2}$n2-n+3与x轴有两个不同的交点A、B，顶点为C．
    （1）求n的取值范围；
    （2）若△ABC的面积是4，求n的值；
    （3）当n取不同的值，抛物线的顶点都在某函数的图象上，试求这个函数的表达式，并求自变量x的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    18．在菱形ABCD中，AB=5，AC=8，点P是AC上的一个动点，过点P作EF垂直于AC交AD于点E，交AB于点F，将△AEF沿EF折叠，使点A落在点A'处，当△A'CD
    是直角三角形时，AP的长为2或$\frac{7}{8}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．2017年5月，一场以“弘扬传统，热爱生活，提升素质，培育人格”为理念，让更多的中学生“爱读国文，乐学国艺”的国学大赛选拔赛，正在如火如荼地在我市某校进行中，在比赛中，有11名学生参加比赛，他们决赛的最终成绩各不相同，其中一名学生想知道自己能否进入前6名，除了要了解自己的成绩外，还要了解这11名学生成绩的（　　）
    A．众数B．方差C．平均数D．中位数

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

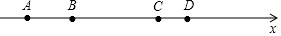
    2．如图，在数轴上有A、B、C、D四个整数点（即各点均表示整数），且2AB=BC=3CD，若A、D两点表示的数分别为-5和6，且AC的中点为E，BD的中点为M，BC之间距点B的距离为$\frac{1}{3}$BC的点N，则该数轴的原点为（　　）
    A．点EB．点FC．点MD．点N

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

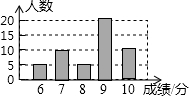    12．如图是根据“红星中学”903班所有学生的立定跳远成绩制作的条形统计图，下列说法中不正确的是（　　）
    A．该校903班有50名学生B．这组数据的众数是7分和8分
    C．这组数据的中位数是9分D．这组数据的平均数是8.4分

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

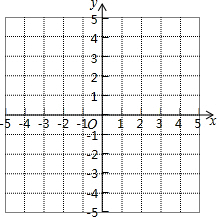    19．小慧根据学习函数的经验，对函数y=|x-1|的图象与性质进行了探究．下面是小慧的探究过程，请补充完成：
    （1）函数y=|x-1|的自变量x的取值范围是任意实数；
    （2）列表，找出y与x的几组对应值．
    x…-10123…
    y…b1012…
    其中，b=2；
    （3）在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
    （4）写出该函数的一条性质：函数的最小值为0（答案不唯一）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．阅读题：$\sqrt{a}$•$\sqrt{b}$=$\sqrt{ab}$（a≥0，b≥0）逆写为$\sqrt{ab}$=$\sqrt{a}$•$\sqrt{b}$（a≥0，b≥0）；$\frac{{\sqrt{a}}}{{\sqrt{b}}}$=$\sqrt{\frac{a}{b}}$（a≥0，b＞0）逆写为$\sqrt{\frac{a}{b}}$=$\frac{{\sqrt{a}}}{{\sqrt{b}}}$（a≥0，b＞0）；（$\sqrt{a}}$）2=a（a≥0）逆写为a=（$\sqrt{a}}$）2（a≥0）．
    应用知识：
    （1）在实数范围内分解因式：x2-2$\sqrt{3}$x+3=（x-$\sqrt{3}$）2；
    （2）化简：$\frac{x-y}{{\sqrt{x}+\sqrt{y}}}$=$\sqrt{x}$-$\sqrt{y}$；
    （3）求值：已知a+b+c-6$\sqrt{a-2}$-10$\sqrt{b+1}$-2$\sqrt{c-3}$=-31，求a+b+c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图是一个底面为正三角形的直三棱柱，则这个几何体的主视图是（　　）
    A．B．C．D．

    查看答案和解析>>

    同步练习册答案