
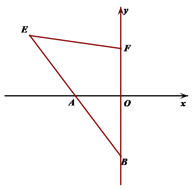
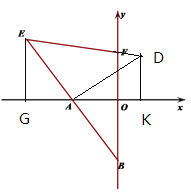
【题目】已知,如图A在x轴负半轴上,B(0,-4),点E(-6,4)在射线BA上,
(1) 求证:点A为BE的中点
(2) 在y轴正半轴上有一点F, 使 ∠FEA=45°,求点F的坐标.
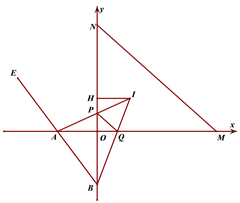
(3) 如图,点M、N分别在x轴正半轴、y轴正半轴上,MN=NB=MA,点I为△MON的内角平分线的交点,AI、BI分别交y轴正半轴、x轴正半轴于P、Q两点, IH⊥ON于H, 记△POQ的周长为C△POQ.求证:C△POQ=2 HI.
【答案】(1)证明见解析;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】试题分析:(1)过E点作EG⊥x轴于G,根据B、E点的坐标,可证明△AEG≌△ABO,从而根据全等三角形的性质得证;
(2)过A作AD⊥AE交EF延长线于D,过D作DK⊥x轴于K,然后根据全等三角形的判定得到△AEG≌△DAK,进而求出D点的坐标,然后设F坐标为(0,y),根据S梯形EGKD=S梯形EGOF+S梯形FOKD可求出F的坐标;
(3)连接MI、NI,根据全等三角形的判定SAS证得△MIN≌△MIA,从而得到∠MIN=∠MIA和∠MIN=∠NIB,由角平分线的性质,求得∠AIB=135°×3-360°=45°再连接OI,作IS⊥OM于S, 再次证明△HIP≌△SIC和△QIP≌△QIC,得到C△POQ周长.
试题解析:(1)过E点作EG⊥x轴于G,
∵B(0,-4),E(-6,4),∴OB=EG=4,
在△AEG和△ABO中,
∵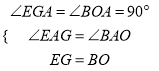
∴△AEG≌△ABO(AAS),∴AE=AB
∴A为BE中点
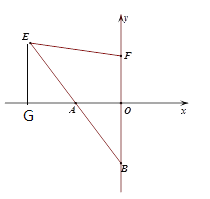
(2)过A作AD⊥AE交EF延长线于D,
过D作DK⊥x轴于K,
∵∠FEA=45°,∴AE=AD,
∴可证△AEG≌△DAK,∴D(1,3),
设F(0,y),
∵S梯形EGKD=S梯形EGOF+S梯形FOKD,
∴![]()
∴![]()
∴![]()
(3)连接MI、NI
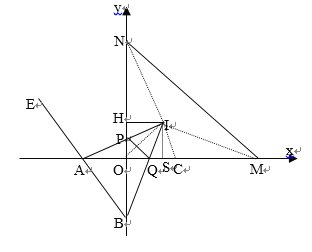
∵I为△MON内角平分线交点,
∴NI平分∠MNO,MI平分∠OMN,
在△MIN和△MIA中,
∵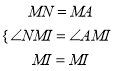
∴△MIN≌△MIA(SAS),
∴∠MIN=∠MIA,
同理可得∠MIN=∠NIB,
∵NI平分∠MNO,MI平分∠OMN,∠MON=90°,
∴∠MIN=135°∴∠MIN=∠MIA =∠NIB=135°,
∴∠AIB=135°×3-360°=45°,
连接OI,作IS⊥OM于S, ∵IH⊥ON,OI平分∠MON,
∴IH=IS=OH=OS,∠HIS=90°,∠HIP+∠QIS=45°,
在SM上截取SC=HP,可证△HIP≌△SIC,∴IP=IC,
∠HIP=∠SIC,∴∠QIC=45°,
可证△QIP≌△QIC,
∴PQ=QC=QS+HP,
∴C△POQ=OP+PQ+OQ=OP+PH+OQ+OS=OH+OS=2HI.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
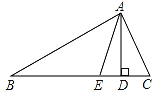
【题目】已知:如图,在△ABC中,AD、AE分别是△ABC的高和角平分线.
(1)若∠B=30°,∠C=50°,求∠DAE的度数.
(2)试问∠DAE与∠C﹣∠B有怎样的数量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一动点P(x,y)从点M(1,0)出发,沿由A(-1,1)、B(-1,-1)、C(1,-1)、D(1,1)四点组成的正方形边线(如图①所示)按一定方向运动.图②是点P运动的路程s(个单位)与运动时间£(秒)之间的函数图象,图③是点P的纵坐标y与点P运动的路程s之间的函数图象的一部分.

(1)s与t之间的函数关系式是_______.
(2)与图③相对应的点P的运动路径是_______;点P出发______秒首次到达点B处.
(3)写出当3≤s≤8时,y与s之间的函数关系式,并在图③中补全函数图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
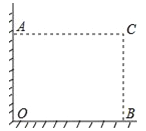
【题目】如图,在直角墙角AOB(OA⊥OB,且OA、OB长度不限)中,要砌20m长的墙,与直角墙角AOB围成地面为矩形的储仓,且地面矩形AOBC的面积为96m2.
(1)求地面矩形AOBC的长;
(2)有规格为0.80×0.80和1.00×1.00(单位:m)的地板砖单价分别为55元/块和80元/块,若只选其中一种地板砖都恰好能铺满储仓的矩形地面(不计缝隙),用哪一种规格的地板砖费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
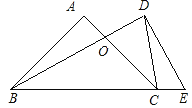
【题目】将一副直角三角板如图摆放,等腰直角三角板ABC的斜边BC与含30°角的直角三角板DBE的直角边BD长度相同,且斜边BC与BE在同一直线上,AC与BD交于点O,连接CD.
求证:△CDO是等腰三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com