练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一次函数的图像经过点（2，2）和（-1，8）．试求：

    （1）这个函数的表达式；

    （2）当 ﹣1＜x＜1时，求 y 的取值范围．

    【答案】（1）y=-2x+6；（2）4＜y＜8

    【解析】试题分析: （1）已知两点，根据待定系数法可以求出解析式.

    （2）根据k的值判断出在每一个象限内函数的增减性，然后将x=-1，1代入函数解析式中求出对应的函数值，进而结合一次函数的增减性进行解答.

    试题解析:

    （1）设y=kx+b,由于图像经过（2,2）和（-1,8）两点,

    ∴

    解得,

    ∴这个函数的表达式是y= -2x+6;

    (2)因为k＜0，故一次函数随着x的增大而减少,

    当x=-1时，y最大，y=8,

    当x= 1时，y最小，y=4

    ∴范围是 4＜y＜8.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】一个不透明的布袋里装有三个球，其中2个红球，1个白球，它们除颜色不同外其余都相同：

    （1）摸出一个球记下颜色后放回，并搅匀，再摸出一个球，求两次摸出的球恰好颜色不同的概率（要求画树状图或列表）；

    （2）现再将n个白球放入布袋中搅匀后使摸出一个球是白球的概率为，求n的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

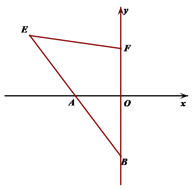
    【题目】已知,如图A在x轴负半轴上，B（0，-4），点E（-6,4）在射线BA上，

    (1) 求证：点A为BE的中点

    (2) 在y轴正半轴上有一点F, 使 ∠FEA=45°，求点F的坐标.

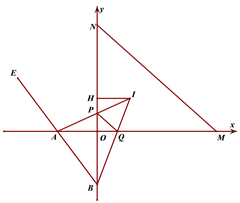
    (3) 如图，点M、N分别在x轴正半轴、y轴正半轴上，MN=NB=MA，点I为△MON的内角平分线的交点，AI、BI分别交y轴正半轴、x轴正半轴于P、Q两点, IH⊥ON于H, 记△POQ的周长为C△POQ.求证：C△POQ=2 HI.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列事件发生的可能性为0的是( )

    A.掷两枚骰子，同时出现数字“6”朝上

    B.小明从家里到学校用了10分钟，从学校回到家里却用了15分钟

    C.今天是星期天，昨天必定是星期六

    D.小明步行的速度是每小时50千米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】【问题提出】

    学习了三角形全等的判定方法（即“SSS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

    【初步思考】

    我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

    【深入探究】

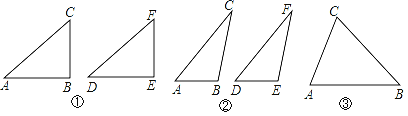
    第一种情况：当∠B是直角时，△ABC≌△DEF．

    如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据　 　，可以知道Rt△ABC≌Rt△DEF．

    第二种情况：当∠B是钝角时，△ABC≌△DEF．

    如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是钝角，请你证明：△ABC≌△DEF（提示：过点C作CG⊥AB交AB的延长线于G，过点F作FH⊥DE交DE的延长线于H）．

    第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

    在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B，∠E都是锐角，请你利用图③，在图③中用尺规作出△DEF，使△DEF和△ABC不全等．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某城市按以下规定收取每月的煤气费：用气不超过60立方米，按每立方米0.8元收费；如果超过60立方米，超过部分按每立方米1.2元收费，已知某用户6月份煤气费平均每立方米0.88元，那么，6月份这位用户应交煤气费多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知：在△ABC中，∠C＝90°，AC＝BC，BD平分∠CBA，DE⊥AB于点E.

    求证：AD＋DE＝BE.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】点（2，-3）关于y轴的对称点是( )

    A. （-2，3） B. （2，3） C. （-2，-3） D. （2，-3）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

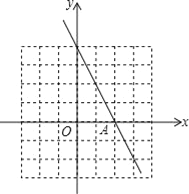
    【题目】已知一次函数y1=kx+b与函数y=﹣2x的图象平行，且与x轴的交点A的横坐标为2．

    （1）求一次函数y1=kx+b的表达式；

    （2）在给定的网格中，画出函数一次函数y2=x+1的图象，并求出一次函数y1=kx+b与y=x+1图象的交点坐标；

    （3）根据图象直接写出，当x取何值时，y1＞y2．

    查看答案和解析>>

    同步练习册答案