
【题目】△ABC中,AB=15,AC=13,高AD=12,则△ABC的周长为( )
A.42
B.32
C.42或32
D.37或33
【答案】C
【解析】解:此题应分两种情况说明:(1)当△ABC为锐角三角形时,在Rt△ABD中, BD= ![]() =
= ![]() =9,
=9,
在Rt△ACD中,
CD= ![]() =
= ![]() =5
=5
∴BC=5+9=14
∴△ABC的周长为:15+13+14=42;(2)当△ABC为钝角三角形时,
在Rt△ABD中,BD= ![]() =
= ![]() =9,
=9,
在Rt△ACD中,CD= ![]() =
= ![]() =5,
=5,
∴BC=9﹣5=4.
∴△ABC的周长为:15+13+4=32
∴当△ABC为锐角三角形时,△ABC的周长为42;当△ABC为钝角三角形时,△ABC的周长为32.
故选C.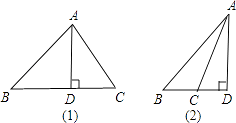
本题应分两种情况进行讨论:(1)当△ABC为锐角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相加即为BC的长,从而可将△ABC的周长求出;(2)当△ABC为钝角三角形时,在Rt△ABD和Rt△ACD中,运用勾股定理可将BD和CD的长求出,两者相减即为BC的长,从而可将△ABC的周长求出.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠AOB,OA=OB,点E在OB上,且四边形AEBF是平行四边形,请你只用无刻度的直尺在图中画出∠AOB的平分线(保留画图痕迹,不写画法),并说明理由. 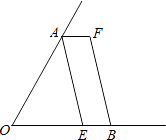
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一人患了流感,经过两轮传染后共有100人患了流感,每轮传染中平均一个人传染的人数x满足的方程为( )
A.1+x+x(1+x)=100
B.x(1+x)=100
C.1+x+x2=100
D.x2=100
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格(每个小正方形边长为1)中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做个点三角形. 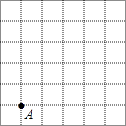
(1)在图中的正方形网格中画出格点△ABC,使AB=3,AC=1(直接画出图形,不写过程);
(2)把你所画的△ABC先向右平移3个单位,再向上平移2个单位,画出平移后的△A1B1C1;
(3)填空BCB1C1 , ∠BAC∠B1A1C1(填“>”“=”“<”).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】作为世界文化遗产的长城,其总长大约为6700000m.数据6700000用科学记数法表( )
A. 6.7×106 B. 67×105 C. 0.67×107D. 6.7×107
查看答案和解析>>
科目:初中数学 来源: 题型:
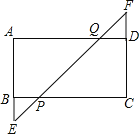
【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=![]() ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=﹣![]() x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
x+2分别与x、y轴交于点B、A,与反比例函数的图象分别交于点C、D,CE⊥x轴于点E,OE=2.
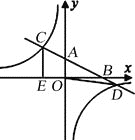
(1)求反比例函数的解析式;
(2)连接OD,求△OBD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com