
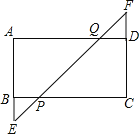
【题目】如图,矩形ABCD中,延长AB至E,延长CD至F,BE=DF,连接EF,与BC、AD分别相交于P、Q两点.
(1)求证:CP=AQ;
(2)若BP=1,PQ=![]() ,∠AEF=45°,求矩形ABCD的面积.
,∠AEF=45°,求矩形ABCD的面积.
【答案】(1)证明见解析;(2)8.
【解析】试题分析:
(1)由矩形的性质得出∠A=∠ABC=∠C=∠ADC=90°,AB=CD,AD=BC,AB∥CD,AD∥BC,证出∠E=∠F,AE=CF,由ASA证明△CFP≌△AEQ,即可得出结论;(2)证明△BEP、△AEQ是等腰直角三角形,得出BE=BP=1,AQ=AE,求出PE=![]() ,得出EQ=PE+PQ=
,得出EQ=PE+PQ=![]() ,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE-BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积;
,由等腰直角三角形的性质和勾股定理得出AQ=AE=3,求出AB=AE-BE=2,DQ=BP=1,得出AD=AQ+DQ=4,即可求出矩形ABCD的面积;
试题解析:
(1)证明:
∵四边形ABCD是矩形
∴∠A=∠ABC=∠C=∠ADC=90°
∴AB=CD,AD=BC,AB∥CD,AD∥BC
∴∠E=∠F
∵BE=DF
∴AE=CF
在△CFP和△AEQ中
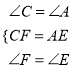
∴△CFP≌△AEQ(ASA)
∴CP=AQ
(2)解:∵AD∥BC
∴∠PBE=∠A=90°
∵∠AEF=45°
∴△BEP、△AEQ是等腰直角三角形
∴BE=BP=1,AQ=AE
∴PE=![]() BP=
BP=![]()
∴EQ=PE+PQ=![]() +2
+2![]() =3
=3![]()
∴AQ=AE=3
∴AB=AE﹣BE=2
∵CP=AQ,AD=BC
∴DQ=BP=1
∴AD=AQ+DQ=3+1=4
∴矩形ABCD的面积=AB×AD=2×4=8.


 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
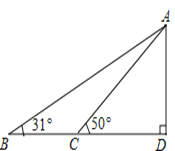
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据调查,超速行驶是引发交通事故的主要原因之一,所以规定以下情境中的速度不得超过15m/s,在一条笔直公路BD的上方A处有一探测仪,如平面几何图,AD=24m,∠D=90°,第一次探测到一辆轿车从B点匀速向D点行驶,测得∠ABD=31°,2秒后到达C点,测得∠ACD=50°(tan31°≈0.6,tan50°≈1.2,结果精确到1m)
(1)求B,C的距离.
(2)通过计算,判断此轿车是否超速.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax+bx+c(a≠0)的图像如图所示,则下列结论中正确的是( )

A.a>0 B.3是方程ax+bx+c=0的一个根
C.a+b+c=0 D.当x<1时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
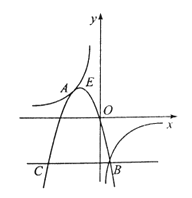
【题目】如图,抛物线![]() 与双曲线
与双曲线![]() 全相交于点A、B,且抛物线经过坐标原点,点
全相交于点A、B,且抛物线经过坐标原点,点![]() 的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
的坐标为(一2,2),点B在第四象限内.过点B作直线BC//x轴,点C为直线BC与抛物线的另一交点,已知直线BC与x轴之间的距离是点B到y轴的距离的4倍.记抛物线顶点为E.
(1)求双曲线和抛物线的解析式;
(2)计算![]() 与
与![]() 的面积;
的面积;
(3)在抛物线上是否存在点D,使![]() 的面积等于
的面积等于![]() 的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
的面积的8倍?若存在,请求出点D的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com