
| A. | a<4 | B. | a≤4 | C. | a>4 | D. | a≥4 |
分析 先求出不等式组中每一个不等式的解集,不等式组有解,即两个不等式的解集有公共部分,据此即可列不等式求得a的范围.
解答 解:$\left\{\begin{array}{l}{1+x<a①}\\{3-x≤0②}\end{array}\right.$
由(1)得x<a-1,
由(2)得x≥3,
∵不等式组$\left\{\begin{array}{l}{1+x<a}\\{3-x≤0}\end{array}\right.$有解,
∴解集应是3≤x<a-1,则a-1>3,
即a>4
实数a的取值范围是a>4.
故选C.
点评 本题是已知不等式组的解集,求不等式中另一未知数的问题.可以先将另一未知数当作已知处理,求出解集与已知解集比较,进而求得另一个未知数.求不等式的公共解,要遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | BC=BA,B′C′=B′A′,∠B=∠B′ | B. | ∠A=∠B′,AC=A′B′,AB=B′C′ | ||
| C. | ∠A=∠A′,AB=B′C′,AC=A′C′ | D. | BC=B′C′,AC=A′B′,∠B=∠C′ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
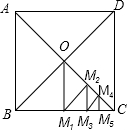 如图,正方形ABCD的边长为4,它的两条对角线交于点O,过点0作边BC的垂线,垂足为M1,△OBM1的面积为S1,过点M1作OC的垂线,垂足为M2,△△OM1M2的面积为S2,过点M2作BC的垂线,垂足为M3,△M1M2M3的面积为S3,…△Mn-2Mn-1Mn的面积为Sn,则S1+S2+S3+…+Sn=( )
如图,正方形ABCD的边长为4,它的两条对角线交于点O,过点0作边BC的垂线,垂足为M1,△OBM1的面积为S1,过点M1作OC的垂线,垂足为M2,△△OM1M2的面积为S2,过点M2作BC的垂线,垂足为M3,△M1M2M3的面积为S3,…△Mn-2Mn-1Mn的面积为Sn,则S1+S2+S3+…+Sn=( )| A. | 4 | B. | 4-($\frac{1}{2}$)n-1 | C. | 4-($\frac{1}{2}$)n-2 | D. | 4-($\frac{1}{2}$)n-3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
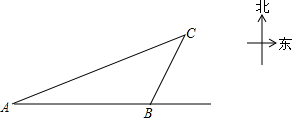 一艘轮船自西向东航行,在A处测得北偏东68.7°方向有一座小岛C,继续向东航行22海里到达B处,测得小岛C此时在轮船的北偏东26.5°方向上,而小岛C方圆10海里的范围内有暗礁,轮船继续向东航行有无触礁的危险呢?请说明理由.(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°≈$\frac{2}{5}$,sin63.5°≈$\frac{9}{10}$,tan63.5°≈2)
一艘轮船自西向东航行,在A处测得北偏东68.7°方向有一座小岛C,继续向东航行22海里到达B处,测得小岛C此时在轮船的北偏东26.5°方向上,而小岛C方圆10海里的范围内有暗礁,轮船继续向东航行有无触礁的危险呢?请说明理由.(参考数据:sin21.3°≈$\frac{9}{25}$,tan21.3°≈$\frac{2}{5}$,sin63.5°≈$\frac{9}{10}$,tan63.5°≈2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com