
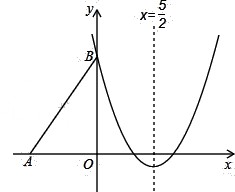
如图,Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,O为坐标 原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线
原点,A、B两点的坐标分别为(﹣3,0)、(0,4),抛物线y=x2+bx+c经过点B,且顶点在直线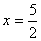 上.
上.
(1)求抛物线对应的函数关系式;
(2)若把△ABO沿x轴向右平移得到△DCE,点A、B、O的对应点分别是D、C、E,当四边形ABCD是菱形时,试判断点C和点D是否在该抛物线上,并说明理由;
(3)在(2)的条件下,连接BD,已知对称轴上存在一点P使得△PBD的周长最小,求出P点的坐标;
科目:初中数学 来源: 题型:
在平行四边形ABCD中,点P从起点B出发,沿BC,CD逆时针方向向终点D匀速运动.设点P所走过的路程为x,则线段AP,AD与平行四边形的边所围成的图形面积为y,表示y与x的函数关系的图象大致如下图,则AB边上的高是
 | |||
 | |||
A.3 B.4 C.5 D.6
查看答案和解析>>
科目:初中数学 来源: 题型:
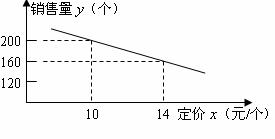
大星发超市进了一批成本为8元/个的文具盒。调查发现:这种文具盒每个星期的 销售量y(个)与它的定价x(元/个)的关系如图所示:
销售量y(个)与它的定价x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销 售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变
售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变
量x的取值范围);
(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
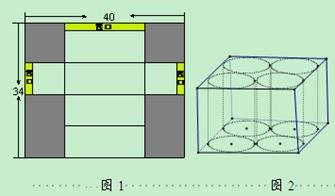
小叶爸爸开了一家茶叶专卖店.包装设计专业毕业的小叶为他爸设计了一款用长方形厚纸片(厚度不计)做长方体茶叶包装盒(如图),阴影部分是裁剪掉的部分.沿图中实线折叠做成的长方体纸盒的上下底面是正方形,有三处矩形形状的“接口”用来折叠后粘贴或封盖.
(1)若小叶用长40cm,宽34cm的矩形厚纸片,恰好能做成 一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“接口”的宽度相等.则该茶叶盒的容积是多少?
一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“接口”的宽度相等.则该茶叶盒的容积是多少?
(2)小叶爸爸的茶叶专卖店以每盒150元购进一批茶叶,按进价增加20%作为售价,第一个月由于包装粗糙,只售出不到一半但超过三分之一的量;第二个月采用了小叶的包装后,马上售完了余下的茶叶,但成本增加了每盒5元,售价仍不变.已知在整个买卖过程中共盈利1500元,求这批茶叶共进了多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中三个分别是正三角形、正方形、正六边形,则另一个是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
查看答案和解析>>
科目:初中数学 来源: 题型:
下列各组图形中,是全等形的是()
A. 两个含60°角的直角三角形
B. 腰对应相 等的两个等腰直角三角形
等的两个等腰直角三角形
C. 边长为3和5的两个等腰三角形
 D. 一个钝角相等的两个等腰三角形
D. 一个钝角相等的两个等腰三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com