
СҶ�ְֿ���һ�Ҳ�Ҷר���꣮��װ���רҵ��ҵ��СҶΪ���������һ���ó����κ�ֽƬ����Ȳ��ƣ����������Ҷ��װ�У���ͼ������Ӱ�����Dzü����IJ��֣���ͼ��ʵ���۵����ɵij�����ֽ�е����µ����������Σ�������������״�ġ��ӿڡ������۵���ճ�����ǣ�
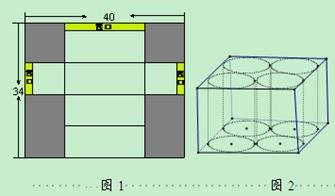
��1����СҶ�ó�40cm����34cm�ľ��κ�ֽƬ��ǡ�������� һ������Ҫ��İ�װ�У��и��Ǻеױ߳���2.5�����������ӿڡ��Ŀ�����ȣ���ò�Ҷ�е��ݻ��Ƕ��٣�
һ������Ҫ��İ�װ�У��и��Ǻеױ߳���2.5�����������ӿڡ��Ŀ�����ȣ���ò�Ҷ�е��ݻ��Ƕ��٣�
��2��СҶ�ְֵIJ�Ҷר������ÿ��150Ԫ����һ����Ҷ������������20%��Ϊ�ۼۣ���һ�������ڰ�װ�ֲڣ�ֻ�۳�����һ�뵫��������֮һ�������ڶ����²�����СҶ�İ�װ���������������µIJ�Ҷ�����ɱ�������ÿ��5Ԫ���ۼ��Բ��䣮��֪���������������й�ӯ��1500Ԫ����������Ҷ�����˶��ٺУ�
�⣺��1���衰�ӿ� ���Ŀ���Ϊxcm���еױ߳�Ϊycm.
���Ŀ���Ϊxcm���еױ߳�Ϊycm.  ��
��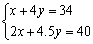 ������������5�֣�
������������5�֣�
���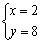 ����8��2.5=20cm��20��8��8=1280cm3�����ò�Ҷ�е��ݻ���1280 cm3������3�֣�
����8��2.5=20cm��20��8��8=1280cm3�����ò�Ҷ�е��ݻ���1280 cm3������3�֣�
��2�����һ����������a�в�Ҷ���ڶ�����������b�в�Ҷ����
150��20%��a+��150��20%��5��b=1500����6a+5b=300����������������������������4�֣�
��a��b��������������ʽ֪aΪ5�ı�������a<b<2a��
��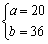 ��
��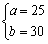 ����a+b=56��55��(3��)
����a+b=56��55��(3��)



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ֱ֪��l1��l2��ֱ��l3��ֱ��l1��l2���ڵ�C��D����ֱ��CD����һ��P��
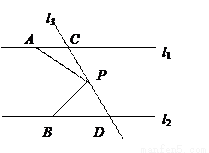
��1�����P����C��D֮���˶�ʱ���ʡ�PAC����APB����PBD��������������ϵ����˵�����ɣ�
��2������P��C��D���������˶�ʱ��P�����C��D���غϣ�����̽����PAC����APB����PBD֮��Ĺ�ϵ������Σ�(��ֱ��д���𰸣�����Ҫ֤��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
С�����ϴӼҳ����ﳵȥ��ѧ��;���������˴�����������ɵ���ѧ��ҵ�����Ǵ�绰���������ϴӼ���������ͬʱС��Ҳ��������������ͣ��˵�˼��仰�����ż����ﳵȥѧУ����С���Ӽҳ���������ʱ��Ϊt��С����ѧУ�ľ���ΪS�������ܷ�ӳS��t�ĺ�����ϵ�Ĵ���ͼ����
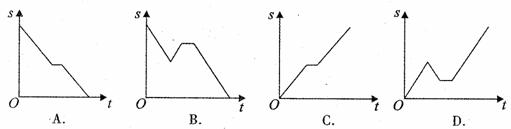
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪��������y=x²+bx+c�����㣨2��-3���ͣ�4��5��.
��1���������ߵı���ʽ���������ꣻ
��2������������x�ᷭ�ۣ��õ�ͼ��G��ͼ��G�ı���ʽ��
��3���ڣ�2���������£���-2<x<2ʱ��ֱ��y=m���ͼ����һ�������㣬��m��ֵ��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��֪ ����������4����ϵʽ����
����������4����ϵʽ����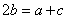 ����
����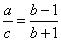 ��
��
��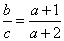 ����
���� ��������ȷ�Ĺ�ϵʽ�����ǣ� ��
��������ȷ�Ĺ�ϵʽ�����ǣ� ��
A. 1 B. 2 C. 3  D. 4
D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
��ͼ��ƽ����4��ֱ��l1��l2�� l3�� l4��һ��ƽ���ߣ�����2��ƽ���ߵľ��붼��1����λ���ȣ�������ABCD��4������A��B��C��D������Щƽ�����ϣ�����������ε�����������ǣ� ��ƽ����λ��
A. 1 B. 3 C. 5 D. 9

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
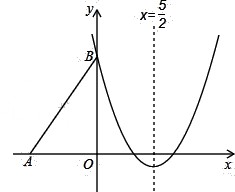
��ͼ��Rt��ABO����ֱ�DZ�OA��OB�ֱ���x��ĸ������y����������ϣ�OΪ���� ԭ�㣬A��B���������ֱ�Ϊ����3��0������0��4����������y=x2+bx+c������B���Ҷ�����ֱ��
ԭ�㣬A��B���������ֱ�Ϊ����3��0������0��4����������y=x2+bx+c������B���Ҷ�����ֱ��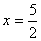 �ϣ�
�ϣ�
��1���������߶�Ӧ�ĺ�����ϵʽ��
��2�����ѡ�ABO��x������ƽ�Ƶõ���DCE����A��B��O�Ķ�Ӧ��ֱ���D��C��E�����ı���ABCD������ʱ�����жϵ�C�͵�D�Ƿ��ڸ��������ϣ���˵�����ɣ�
��3���ڣ�2���������£�����BD����֪�Գ����ϴ���һ��Pʹ�á�PBD���ܳ���С�����P������ꣻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
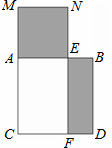
��֪�߶�AB�ij�Ϊ1����ABΪ����AB���·���������ACDB��ȡA B����һ��E����AEΪ����AB���Ϸ���������AENM����E��EF�ACD������ΪF�㣮��������AENM���ı���EFDB�������ȣ���AE�ij�Ϊ _��
B����һ��E����AEΪ����AB���Ϸ���������AENM����E��EF�ACD������ΪF�㣮��������AENM���ı���EFDB�������ȣ���AE�ij�Ϊ _��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com