
已知:抛物线y=x²+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图像G求图像G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图像有一个公共点,求m的值或取值范围.
解:(1)把(2,-3)和(4,5)分别代入y=x²+bx+c
 得:
得: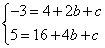 ,解得:
,解得: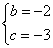 ,
,
∴抛物线的表达式为:y=x²-2x-3. …………………………………2分.
∵y=x²-2x-3=(x-1)2-4.
∴顶点坐标为(1,-4). …………………………………3分.
(2)∵将抛物线沿x轴翻折,得到图像G与原抛物线图形
关于x轴对称,
∴图像G的表达式为:y=-x²+2x+3. ………………………5分.
(3)如图,当0≤x<2时,y=m过抛物线顶点(1,4)时,
直线y=m与该图像有一个公共点,此时y=4,∴m=4.
当-2<x<0时,直线y=m与该图像有一个公共点,
当y=m过抛物线上的点(0,3)时, y=3,∴m=3.
当y=m过抛物线上的点(-2,-5)时, y=-5,∴m=-5.
∴-5<m<3.
综上:m的值为4,或-5<m≤3. …………………………………7分.


科目:初中数学 来源: 题型:
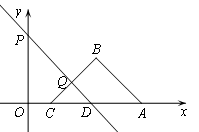
如图,在平面直角 坐标系中,点 A(5,0),B(3,2),点C在线段OA上,BC=BA,点Q是线段BC上一个动点,点P的坐标是(0,3),直线PQ的解析式为y=kx+b(k≠0),且与x轴交于点D.
坐标系中,点 A(5,0),B(3,2),点C在线段OA上,BC=BA,点Q是线段BC上一个动点,点P的坐标是(0,3),直线PQ的解析式为y=kx+b(k≠0),且与x轴交于点D.
(1)求点C的坐标及b的值;
(2)求k的取值范围;
(3)当k为取值范围内的最大整数时,过点B作BE∥x轴,交PQ于点E,若抛物线y=ax2﹣5ax(a≠0)的顶点在四边形ABED的内部,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
观察下列一组坐标:
(a,b),(a,c),(b,c),(b,a),(c,a),(c,b),(a,b),(a,c)…… ,它们是按一定规律排列的,那么第9个坐标是 ,第2015个坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
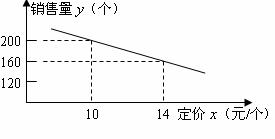
大星发超市进了一批成本为8元/个的文具盒。调查发现:这种文具盒每个星期的 销售量y(个)与它的定价x(元/个)的关系如图所示:
销售量y(个)与它的定价x(元/个)的关系如图所示:
(1)求这种文具盒每个星期的销 售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变
售量y(个)与它的定价x(元/个)之间的函数关系式(不必写出自变
量x的取值范围);
(2)每个文具盒定价是多少元时,超市每星期销售这种文具盒(不考虑其他因素)可获得的利润最高?最高利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
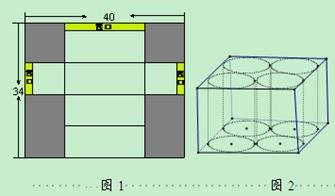
小叶爸爸开了一家茶叶专卖店.包装设计专业毕业的小叶为他爸设计了一款用长方形厚纸片(厚度不计)做长方体茶叶包装盒(如图),阴影部分是裁剪掉的部分.沿图中实线折叠做成的长方体纸盒的上下底面是正方形,有三处矩形形状的“接口”用来折叠后粘贴或封盖.
(1)若小叶用长40cm,宽34cm的矩形厚纸片,恰好能做成 一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“接口”的宽度相等.则该茶叶盒的容积是多少?
一个符合要求的包装盒,盒高是盒底边长的2.5倍,三处“接口”的宽度相等.则该茶叶盒的容积是多少?
(2)小叶爸爸的茶叶专卖店以每盒150元购进一批茶叶,按进价增加20%作为售价,第一个月由于包装粗糙,只售出不到一半但超过三分之一的量;第二个月采用了小叶的包装后,马上售完了余下的茶叶,但成本增加了每盒5元,售价仍不变.已知在整个买卖过程中共盈利1500元,求这批茶叶共进了多少盒?
查看答案和解析>>
科目:初中数学 来源: 题型:
一幅美丽的图案,在某个顶点处由四个边长相等的正多边形镶嵌而成,其中三个分别是正三角形、正方形、正六边形,则另一个是( )
A.正三角形 B.正方形 C.正五边形 D.正六边形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com