练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    对于公式，若已知和，求=__________


     


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    在市委宣传部举办的以“弘扬社会主义核心价值观”为主题的演讲比赛中，其中10位参赛选手的成绩如下：9.3；9.5；8.9；9.3；9.5；9.5；9.7；9.4；9.5，这组数据的众数是　

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图是一个几何体的三视图，则这个几何体的侧面积是

        A cm2   B.  cm2    C. 6cm2    D．3cm2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，抛物线y=ax2 +bx+c经过点A(-3，0)、C(0，4)，点B在抛物线上，CB

    ∥X轴．且AB平分∠CAO.

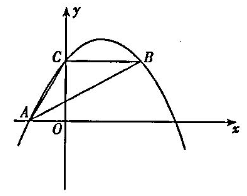
        (1)求抛物线的解析式．

        (2)线段AB上有一动点P，过P作y轴的平行线，交抛物线于点Q，求线段PQ的最大值；

    (3)抛物线的对称轴上是否存在点M，使△ABM是以AB为直角边的直角三角形？如果存在，直接写出点M的坐标；如果不存在，说明理由，

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在边长为a的正方形中挖去一个边长为b的小正方形（a＞b）（如图1），把余下的部分拼成一个梯形（如图2），根据两个图形中阴影部分的面积相等，可以验证                                          （　　）

    （A）a2－b2＝(a＋b)(a－b)

    （B）(a－b)2＝a2－2ab＋b2

    （C）(a＋b)2＝a2＋2ab＋b2

    （D）(a＋2b)(a－b)＝a2＋ab－2b2

     




    查看答案和解析>>

    科目：初中数学 来源： 题型：


              

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知直线l1∥l2，直线l3和直线l1、l2交于点C和D，在直线CD上有一点P．

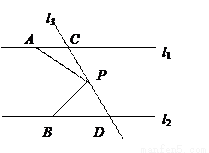
    （1）如果P点在C、D之间运动时，问∠PAC，∠APB，∠PBD有怎样的数量关系？请说明理由．

    （2）若点P在C、D两点的外侧运动时（P点与点C、D不重合），试探索∠PAC，∠APB，∠PBD之间的关系又是如何？(请直接写出答案，不需要证明)

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，这个二次函数图象的表达式可能是           ．（只写出一个）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知：抛物线y=x²+bx+c经过点（2，-3）和（4，5）.

    （1）求抛物线的表达式及顶点坐标；

    （2）将抛物线沿x轴翻折，得到图像G求图像G的表达式；

    （3）在（2）的条件下，当-2<x<2时，直线y=m与该图像有一个公共点，求m的值或取值范围.

    查看答案和解析>>

    同步练习册答案